
【题目】已知函数f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)对任意![]() ,
,![]() 都有恒成立,求实数a的取值范围;
都有恒成立,求实数a的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)![]() (2)(
(2)(![]() (3)见证明
(3)见证明
【解析】
(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律确定函数单调性,最后根据函数单调性确定最小值取法;(2)先分离不等式,转化为对应函数最值问题,利用导数求对应函数最值即得结果;(3)构造两个函数,再利用两函数最值关系进行证明.
(1)![]()
当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增,所以函数f(x)的最小值为f(
单调递增,所以函数f(x)的最小值为f(![]() )=
)=![]() ;
;
(2)因为![]() 所以问题等价于
所以问题等价于![]() 在
在![]() 上恒成立,
上恒成立,
记![]() 则
则![]() ,
,
因为![]() ,
,
令![]()
![]() 函数f(x)在(0,1)上单调递减;
函数f(x)在(0,1)上单调递减;
![]() 函数f(x)在(1,+
函数f(x)在(1,+![]() )上单调递增;
)上单调递增;
![]() 即
即![]() ,
,
即实数a的取值范围为(![]() .
.
(3)问题等价于证明![]()
由(1)知道![]()
![]() ,令
,令![]()
![]() 函数
函数![]() 在(0,1)上单调递增;
在(0,1)上单调递增;
![]() 函数
函数![]() 在(1,+
在(1,+![]() )上单调递减;
)上单调递减;
所以{![]() ,
,
因此![]() ,因为两个等号不能同时取得,所以
,因为两个等号不能同时取得,所以![]()
即对一切![]() ,都有
,都有![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (
(![]() 为参数),直线l与曲线C分别交于M,N两点.
为参数),直线l与曲线C分别交于M,N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若点![]() ,求
,求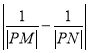 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有7个点,每三点的两两连线都组成一个不等边三角形.求证:一定可以找到4对三角形,使每对三角形的公共边既是其中一个三角形的最长边又是另一个三角形的最短边.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两名射击运动员分别对一目标射击一次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)2人都射中目标的概率;
(2)2人中恰有1人射中目标的概率;
(3)2人至少有1人射中目标的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com