
| | 理科 | 文科 | 合计 |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
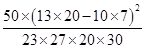 ≈4.844,则认为选修文科与性别有关系出错的可能性约为______.
≈4.844,则认为选修文科与性别有关系出错的可能性约为______. 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.9 | B.8 | C.7 | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
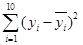 的值为( )
的值为( )| A.241.1 | B.245.1 | C.2411 | D.2451 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
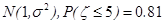 ,则
,则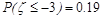 ;
;| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 嗜酒 | 不嗜酒 | 总计 |
| 患肝病 | 7 775 | 42 | 7 817 |
| 未患肝病 | 2 099 | 49 | 2 148 |
| 总计 | 9 874 | 91 | 9 965 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
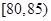 ,
,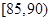 ,
, ,
,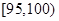 ,
,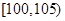 ,
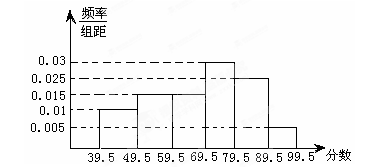
,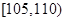 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.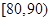 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在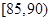 的车辆数
的车辆数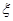 的分布列及数学期望.
的分布列及数学期望.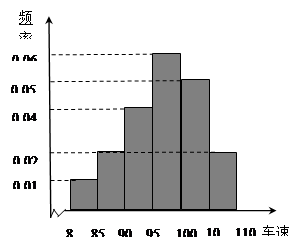
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com