
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() 是线段
是线段![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)在已知极坐标方程两边同时乘以ρ后,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2可得曲线C的直角坐标方程;
(2)联立直线l的参数方程与x2=4y由韦达定理以及参数的几何意义和弦长公式可得弦长与已知弦长相等可解得.
解:(1)在ρ+ρcos2θ=8sinθ中两边同时乘以ρ得ρ2+ρ2(cos2θ﹣sin2θ)=8ρsinθ,
∴x2+y2+x2﹣y2=8y,即x2=4y,
所以曲线C的直角坐标方程为:x2=4y.
(2)联立直线l的参数方程与x2=4y得:(cosα)2t2﹣4(sinα)t+4=0,
设A,B两点对应的参数分别为t1,t2,
由△=16sin2α﹣16cos2α>0,得sinα>![]() ,
,
t1+t2=![]() ,由|PM|=
,由|PM|=![]() ,
,
所以20sin2α+9sinα﹣20=0,解得sinα=![]() 或sinα=﹣
或sinα=﹣![]() (舍去),
(舍去),
所以sinα=![]() .
.


科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() ,
,
![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
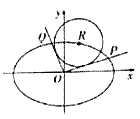
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上的动点,由原点
上的动点,由原点![]() 向圆
向圆![]() 引两条切线,分别交椭圆于点
引两条切线,分别交椭圆于点![]() ,若直线
,若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,试问
,试问![]() 的面积是否为定值?若是,求出该值;若不是,请说明理由.
的面积是否为定值?若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为4,E、F分别是棱AB、
的棱长为4,E、F分别是棱AB、![]() 的中点,联结EF、
的中点,联结EF、![]() 、
、![]() 、
、![]() E、
E、![]() E、
E、![]() E.
E.

![]() 求三棱锥
求三棱锥![]() 的体积;
的体积;
![]() 求直线
求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间做A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1小时和2小时,漆工油漆一张A,B型桌子分别需要3小时和1小时;又知木工和漆工每天工作分别不得超过8小时和9小时,设该厂每天做A,B型桌子分别为x张和y张.
(1)试列出x,y满足的关系式,并画出相应的平面区域;
(2)若工厂做一张A,B型桌子分别获得利润为2千元和3千元,那么怎样安排A,B型桌子生产的张数,可使得所得利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com