
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为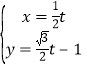 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为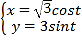 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中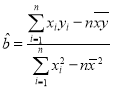 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题是真命题
”的逆否命题是真命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
C. 若![]() 为真命题,则
为真命题,则![]() 为真命题
为真命题
D. 已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):
甲班:82 84 85 89 79 80 91 89 79 74
乙班:90 76 86 81 84 87 86 82 85 83
(1)求两个样本的平均数;
(2)求两个样本的方差和标准差;
(3)试分析比较两个班的学习情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=ax+(1﹣a)lnx+![]() (a∈R)
(a∈R)
(Ⅰ)当a=0时,求 f(x)的极值;
(Ⅱ)当a<0时,求 f(x)的单调区间;
(Ⅲ)方程 f(x)=0的根的个数能否达到3,若能请求出此时a的范围,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有20张卡片分别写着数字1,2,…,19,20,将它们放入一个盒中,有4个人从中各抽取一张卡片,取到两个较小数字的二人在同一组,取得两个较大数字的二人在同一组,若其中二人分别抽到5和14,则此二人在同一组的概率等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com