
| A. | 9 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求最大值m,然后根据基本不等式的性质进行求解即可.
解答 解:作出不等式组对应的平面区域如图:(阴影部分)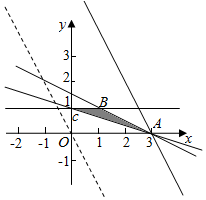
由z=2x+y得y=-2x+z,平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A(3,0)时,直线y=-2x+z的截距最大,此时z最大.
代入目标函数z=2x+y得z=2×3=6.
即m=6.
则a+b=6,
∴$\frac{1}{a}+\frac{4}{b}$=$\frac{1}{6}$($\frac{1}{a}+\frac{4}{b}$)(a+b)=$\frac{1}{6}$(1+4+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{1}{6}$(5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$)=$\frac{3}{2}$,当且仅当a=2,b=4取等号,
故选:B
点评 本题主要考查线性规划以及基本不等式的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“$?{x_0}∈R,{x_0}^2+1>3{x_0}$”的否定是“$?{x_0}∈R,{x^2}+1>3x$” | |
| B. | “函数f(x)=cosax-sinax的最小正周期为 π”是“a=2”的必要不充分条件 | |
| C. | x2+2x≥ax在x∈[1,2]时有解?(x2+2x)min≥(ax)min在x∈[1,2]时成立 | |
| D. | “平面向量$\overrightarrow a$与$\overrightarrow b$的夹角是钝角”的充分必要条件是“$\overrightarrow a$•$\overrightarrow b$<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
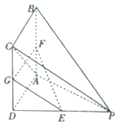 如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com