
 如图,点A在⊙O上,过点O的割线PBC交⊙O于点B,C,且PA=4,PB=2,OB=3,∠APC的平分线分别交AB,AC于D,E.
如图,点A在⊙O上,过点O的割线PBC交⊙O于点B,C,且PA=4,PB=2,OB=3,∠APC的平分线分别交AB,AC于D,E.分析 (1)由弦切角定理得∠BAP=∠C,从而∠BAP+∠APD=∠C+∠CPE,由此能证明∠ADE=∠AED.
(2)利用角平分线的性质得到比值相等,即可证明结论.
解答  证明:(1)连接OA,
证明:(1)连接OA,
∵AP2+OA2=16+9=25=(OB+BP)2,
∴OA⊥AP,
∴PA为⊙O的切线,
∴∠PAB=∠C,
∵∠AEP=∠C+∠BPE,∠ADE=∠PAB+∠APE,
∵PE平分∠APC,
∴∠BPE=∠APE
∴∠ADE=∠AED;
(2)∵PE是∠APC的平分线,
∴$\frac{AD}{DB}$=$\frac{AP}{PB}$=$\frac{4}{2}$,$\frac{EC}{EA}=\frac{PC}{PA}$=$\frac{4}{2}$,
∴$\frac{AD}{DB}$=$\frac{EC}{EA}$,
∴AD•AE=BD•CE.
点评 本题考查两角相等的证明,考查角平分线的性质的运用,是中档题,解题时要认真审题,注意弦切角定理、角平分线的性质、圆的性质等知识点的合理运用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{π}^{2}}{4}$+1 | B. | $\frac{{π}^{2}}{4}$-1 | C. | $\frac{3{π}^{2}}{8}$-1 | D. | $\frac{3{π}^{2}}{8}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | $\frac{{\sqrt{2}}}{2}a$ | B. | $\frac{{3\sqrt{2}}}{2}a$ | C. | $\frac{{\sqrt{3}}}{2}a$ | D. | $\frac{{\sqrt{6}}}{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 20 | C. | 19 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
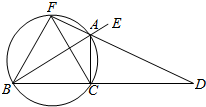 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
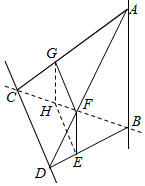 如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.
如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.
如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com