练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC的两边长分别为2,3，其夹角的余弦值为，则其外接圆的半径
    为（  )
    A．B．C．D．
    C
    分析：先利用余弦定理求得三角形第三边长，进而根据同角三角函数的基本关系求得第三边所对角的正弦，最后利用正弦定理求得外接圆的半径．
    解答：解：由余弦定理得：三角形第三边长为
    =3，
    且第三边所对角的正弦值为=，
    所以由正弦定理可知2R=，求得R=
    故选C
    点评：本题主要考查了正弦定理和余弦定理的应用．作为解三角形问题常用公式如正弦定理和余弦定理公式，勾股定理，三角形面积公式等，应作为平时训练的重点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在△ABC中，角A、B、C所对的边分别是a，b，c，若b2＋c2－bc＝a 2，且＝，则角B的值为(　　　)
    A．30°B．45°C．90°D．120°

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

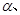
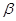    已知偶函数y=f(x)在区间〔-1,0〕是减函数,又是锐角三角形的两个内角,则（ ）
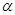    A  f(sin)＞f(cos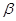)     B　 f(sin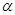)＜ f(cos)
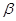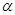    C 　f(sin)＞f(sin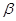)     D　　f(cos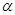)＜f(cos)

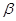    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在中，，则等于（   ）
                     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    设三角形的内角的对边分别为 ,．
    （1）求边的长；
    （2）求角的大小。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

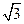    甲船在A处观察乙船，乙船在它的北偏东60°的方向，两船相距a海里，乙船正向北行驶，若甲船是乙船速度的倍，甲船为了尽快追上乙船，则应取北偏东________（填角度）的方向前进。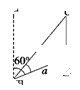

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在△中，如果三边依次成等比数列，那么角的取值范围是         ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某舰艇在A处测得遇险渔船在北偏东距离为10海里的C处，此时得知，该渔船沿北偏东方向，以每小时9海里的速度向一小岛靠近，舰艇时速21海里，则舰艇到达渔船的最短时间是___________．

    查看答案和解析>>

    同步练习册答案