
【题目】已知椭圆![]() :
:![]() ,过椭圆右焦点的最短弦长是
,过椭圆右焦点的最短弦长是![]() ,且点
,且点 在椭圆上.
在椭圆上.
(1)求该椭圆的标准方程;
(2)设动点![]() 满足:
满足:![]() ,其中
,其中![]() ,
,![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,求点
,求点![]() 的轨迹方程并判断是否存在两个定点
的轨迹方程并判断是否存在两个定点![]() 、
、![]() ,使得
,使得![]() 为定值?若存在,求出定值;若不存在,说明理由.
为定值?若存在,求出定值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若数列![]() 为递增数列且
为递增数列且![]() ,设
,设![]() ,试问是否存在正整数
,试问是否存在正整数![]() (其中
(其中![]() ),使
),使![]() 成等比数列?若存在,求出所有满足条件的数组
成等比数列?若存在,求出所有满足条件的数组![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,椭圆上的点到左焦点的最小值为
,椭圆上的点到左焦点的最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为直线
为直线![]() 上任意一点,设直线
上任意一点,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,记
,记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 恒成立?若是,请求出
恒成立?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
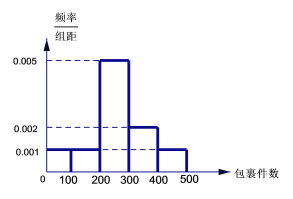
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: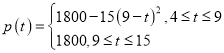 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东方商店欲购进某种食品(保质期两天),此商店每两天购进该食品一次(购进时,该食品为刚生产的).根据市场调查,该食品每份进价![]() 元,售价
元,售价![]() 元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区
元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区![]() 天的销售量如下表:
天的销售量如下表:

(视样本频率为概率)
(1)根据该产品![]() 天的销售量统计表,记两天中一共销售该食品份数为
天的销售量统计表,记两天中一共销售该食品份数为![]() ,求
,求![]() 的分布列与期望
的分布列与期望
(2)以两天内该产品所获得的利润期望为决策依据,东方商店一次性购进![]() 或
或![]() 份,哪一种得到的利润更大?
份,哪一种得到的利润更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com