
【题目】设甲、乙、丙3个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这3个协会中抽取6名运动员组队参加比赛.
(1)求应从这3个协会中分别抽取的运动员的人数.
(2)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率.
【答案】(1) 从甲、乙、丙三个协会中抽取的运动员人数分别为3,1,2;(2)①见解析;②![]() .
.
【解析】试题分析:(1)由题为分层抽样,可知每个个体被抽到的可能性相同.则可得概率为![]() ;
;
(2)(i)用所给编号列出所有可能的结果则为6个元素中取出2个的所有情况可列出;
(ii)为古典概型,可结合上问中的结论,确定所包含的基本事件,代入古典概率公式可得。
试题解析:(Ⅰ)分层抽样中,每个个体被抽到的可能性相同
乙乒乓球协会的某运动员被抽到的概率![]()
(Ⅱ)(i)从6名运动员中随机抽取2名的所有结果为:
(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),
(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),
(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6),共15种;
(ii)设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”,
则事件A包含:(A1,A5),(A1,A6),(A2,A5),(A2,A6),
(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6)共9个基本事件,
∴事件A发生的概率P=![]() =
=![]()


科目:高中数学 来源: 题型:
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为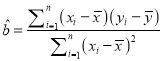 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 在
在![]() 上存在极值点,求
上存在极值点,求![]() 的取值范围;
的取值范围;
(2)设![]() ,
, ![]() ,若
,若![]() 存在最大值,记为
存在最大值,记为![]() ,则当
,则当![]() 时,
时, ![]() 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
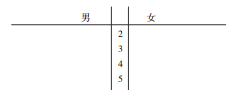
【题目】某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有30份给予回复,这30份的评分如下:

(Ⅰ)完成下面的茎叶图,并求16名男消费者评分的中位数与14名女消费者评分的平均值;

(Ⅱ)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.
参考公式:  ,其中
,其中![]()
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学课上,老师为了提高同学们的兴趣,先让同学们从1到3循环报数,结果最后一个同学报2;再让同学们从1到5循环报数,最后一个同学报3;又让同学们从1到7循报数,最后一个同学报4.请你设计一个算法,计算这个班至少有多少人,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
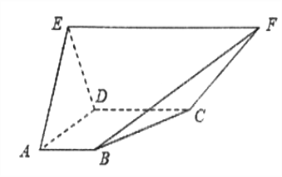
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com