
【题目】现有一个关于平面图形的命题:如图,同一平面内有两个边长都是2的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为______.
【答案】1
【解析】
连OA,OB,设OR交BC于M,OP交AB于N,由四边形ABCD为正方形,得到OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,而四边形ORQP为正方形,得∠NOM=90°,所以∠MOB=∠NOA,则△OBM≌△OAN,即可得到S四边形MONB=S△AOB.
解:连OA,OB,设OR交BC于M,OP交AB于N,
如图示:
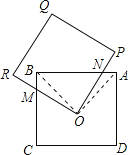
∵四边形ABCD为正方形,
∴OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,
而四边形ORQP为正方形,
∴∠NOM=90°,
∴∠MOB=∠NOA,
∴△OBM≌△OAN,
∴S四边形MONB=S△AOB![]() 2×2=1,
2×2=1,
即它们重叠部分的面积为1,
故答案为:1


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如果一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“阿当数列”.
(1)若数列![]() 为“阿当数列”,且
为“阿当数列”,且![]() ,
,![]() ,
,![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)是否存在首项为1的等差数列![]() 为“阿当数列”,且其前
为“阿当数列”,且其前![]() 项和
项和![]() 满足
满足![]() ?若存在,请求出
?若存在,请求出![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)已知等比数列![]() 的每一项均为正整数,且
的每一项均为正整数,且![]() 为“阿当数列”,
为“阿当数列”,![]() ,
,![]() ,当数列
,当数列![]() 不是“阿当数列”时,试判断数列
不是“阿当数列”时,试判断数列![]() 是否为“阿当数列”,并说明理由.
是否为“阿当数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有穷数列![]() 中的每一项都是-1,0,1这三个数中的某一个数,
中的每一项都是-1,0,1这三个数中的某一个数,![]() ,且
,且![]()
![]()
![]() ,则有穷数列
,则有穷数列![]() 中值为0的项数是( )
中值为0的项数是( )
A. 1000B. 1010C. 1015D. 1030
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过点
过点![]() 并且与圆
并且与圆![]() 相外切,动圆圆心
相外切,动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,设直线
两点,设直线![]() ,设点
,设点![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,求证:直线
,求证:直线![]() 经过定点
经过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)将曲线![]() 经过伸缩变换
经过伸缩变换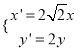 后得到曲线
后得到曲线![]() ,若
,若![]() ,
, ![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com