
分析 由求导公式和法则求出f′(x),把x=1代入求出f′(1)的值,再求出程f′(x)=0的解集.
解答 解:由题意得,f′(x)=$\frac{1}{x}$+2x•f′(1),
则f′(1)=1+2f′(1),解得f′(1)=-1,
所以f′(x)=$\frac{1}{x}$-2x,
由f′(x)=$\frac{1}{x}$-2x=0得,${x}^{2}=\frac{1}{2}$,则x=$±\frac{\sqrt{2}}{2}$,
又x=$-\frac{\sqrt{2}}{2}$<0舍去,
所以方程f′(x)=0的解集为$\left\{{\frac{{\sqrt{2}}}{2}}\right\}$,
故答案为:$\{\frac{\sqrt{2}}{2}\}$.
点评 本题考查导数的运算,以及方程思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
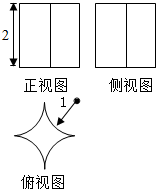 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  圆形区域 | |
| B. |  等腰三角形两腰与半椭圆围成的区域 | |
| C. | 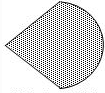 等腰三角形两腰与半圆围成的区域 | |
| D. | 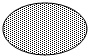 椭圆形区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递增函数 | B. | 单调递减函数 | C. | 先减后增函数 | D. | 先增后减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
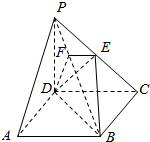 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com