


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
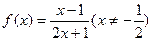 的对称中心是
的对称中心是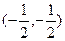 ;③对任意实数a,b则
;③对任意实数a,b则 ④取一根长为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不少于1m的概率是
④取一根长为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不少于1m的概率是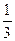 ;⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则△A1B1C1为锐角三角形,△A2B2C2为钝角三角形.其中真命题的序号是 (将所有真命题的序号都填上).
;⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则△A1B1C1为锐角三角形,△A2B2C2为钝角三角形.其中真命题的序号是 (将所有真命题的序号都填上). 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
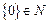 ;③ 这是一颗大树;④
;③ 这是一颗大树;④  ;⑤
;⑤  ⑥ 老年人组成一个集合;
⑥ 老年人组成一个集合;| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
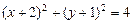 与直线
与直线 相交,所得弦长为2;②直线
相交,所得弦长为2;②直线 与圆
与圆 恒有公共点;③若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为108
恒有公共点;③若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为108 ;④若棱长为
;④若棱长为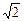 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为 其中,正确命题的序号为 .写出所有正确命的序号)
其中,正确命题的序号为 .写出所有正确命的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com