
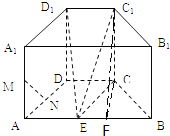
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分别是棱AA1、AD的中点,设E是棱AB的中点. 
(1)求证:MN∥平面CEC1;
(2)求平面D1EC1与平面ABCD所成角的正切值.
【答案】
(1)证明:∵在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,
AB∥CD,AB=4,BC=CD=2,AA1=2,
M、N分别是棱AA1、AD的中点,设E是棱AB的中点,
∴DD1∥CC1,AD∥CE,
∵AD∩DD1=D,CC1∩CE=C,
AD,DD1平面A1DD1A,CC1,CE平面CEC1,
∴平面A1DD1A∥平面CEC1,
∵MN平面A1DD1A,∴MN∥平面CEC1
(2)解:平面D1EC1与平面ABCD所成角就是平面ABC1D1与平面ABCD所成的角,
∵CC1⊥平面ABCD,过C作CF⊥AB,交AB于F,连结C1F,
则∠CFC1是平面D1EC1与平面ABCD所成角,
∵CC1=AA1=2,CE=BC=BE=2,CF= ![]() =
= ![]() ,
,
∴tan∠CFC1= ![]() =
= ![]() =
= ![]() .
.
∴平面D1EC1与平面ABCD所成角的正切值为 ![]()
【解析】(1)推导出DD1∥CC1 , AD∥CE,从而平面A1DD1A∥平面CEC1 , 由此能证明MN∥平面CEC1 . (2)平面D1EC1与平面ABCD所成角就是平面ABC1D1与平面ABCD所成的角,过C作CF⊥AB,交AB于F,连结C1F,则∠CFC1是平面D1EC1与平面ABCD所成角,由此能求出平面D1EC1与平面ABCD所成角的正切值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学玩游戏,对于给定的实数a1 , 按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把a1乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把a1除以2后再加上12,这样就可以得到一个新的实数a2 , 对实数a2仍按上述方法进行一次操作,又得到一个新的实数a3 , 当a3>a1 , 甲获胜,否则乙获胜,若甲获胜的概率为 ![]() ,则a1的取值范围是( )
,则a1的取值范围是( )
A.(﹣∞,12]
B.[24,+∞)
C.(12,24)
D.(﹣∞,12]∪[24,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M(x,y)在|x|≤1,|y|≤1时按均匀分布出现,试求满足:
(1)x+y≥0的概率;
(2)x+y<1的概率;
(3)x2+y2≥1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com