Question

【题目】已知不等式x2+mx+3≤0的解集为A=[1，n]，集合B={x|x2﹣ax+a≤0}．
（1）求m﹣n的值；
（2）若A∪B=A，求a的取值范围．

Answer 1

【答案】
（1）解：∵不等式x2+mx+3≤0的解集为A=[1，n]，

∴ ，∴m=﹣4，n=3，

∴m﹣n=﹣7；

（2）解：A∪B=A，∴BA．

①B=，△=a2﹣4a＜0，∴0＜a＜4；

②B≠，设f（x）=x2﹣ax+a，则 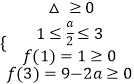，∴4≤a≤ ，

综上所述，0＜a≤ ．

【解析】本题考查的是集合的运算性质A∪B=A，BA．尤其是当B=的时候以及一元二次不等式代入特殊值的解法。
【考点精析】关于本题考查的解一元二次不等式，需要了解求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边才能得出正确答案．