
【题目】(本小题满分12分)已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)因为函数在定义域内有两个不同的极值点,所以导函数等于![]() 的方程有两个不等的实根,再通过分离转化为两个基本函数有两个不同的交点,函数与直线相切时为临界值;(2)因为
的方程有两个不等的实根,再通过分离转化为两个基本函数有两个不同的交点,函数与直线相切时为临界值;(2)因为![]() 是两个极值点,代入方程
是两个极值点,代入方程![]() ,由参变分离,可以把
,由参变分离,可以把![]() 用
用![]() 来表示.要证
来表示.要证![]() ,即证
,即证![]() ,即
,即![]() ,把
,把![]() 用
用![]() 换掉,变量集中构造新函数求导判断单调性求出最值.
换掉,变量集中构造新函数求导判断单调性求出最值.
试题解析:解:(1)依题意,函数![]() 的定义域为
的定义域为![]() ,∴方程
,∴方程![]() 在
在![]() 上有两个不同根,
上有两个不同根,
即方程![]() 在
在![]() 上有两个不同根.
上有两个不同根.
转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,如图,
上有两个不同交点,如图,
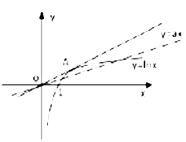
可见,若令过原点且切于函数![]() 图象的直线斜率为
图象的直线斜率为![]() ,只需
,只需![]() .
.
令切点![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
于是![]() ,∴
,∴![]() .
.
(2)由(1)可知![]() 分别是方程
分别是方程![]() 的两根,即
的两根,即![]() ,
,![]() ,
,
设![]() ,作差得
,作差得![]() ,即
,即 .
.
原不等式![]() 等价于
等价于![]()
令![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即不等式
,即不等式![]() 成立,
成立,
故所证不等式![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(I)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(II)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() .设点
.设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需用![]() 两种原料,已知每种产品各生产
两种原料,已知每种产品各生产![]() 吨所需原料及每天原料的可用限额如下表所示,如果生产
吨所需原料及每天原料的可用限额如下表所示,如果生产![]() 吨甲产品可获利润3万元,生产
吨甲产品可获利润3万元,生产![]() 吨乙产品可获利
吨乙产品可获利![]() 万元,则该企业每天可获得最大利润为___________万元.
万元,则该企业每天可获得最大利润为___________万元.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆八中大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间及所有零点;
的单调区间及所有零点;
(2)设![]() ,
,![]() ,
,![]() 为函数
为函数![]() 图象上的三个不同点,且
图象上的三个不同点,且
![]() .问:是否存在实数
.问:是否存在实数![]() ,使得函数
,使得函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行?若存在,求出所有满足条件的实数
平行?若存在,求出所有满足条件的实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com