
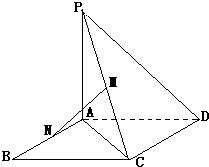
 16、如图,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N分别为PC,AB中点,求证:MN⊥P C.
16、如图,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N分别为PC,AB中点,求证:MN⊥P C. 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
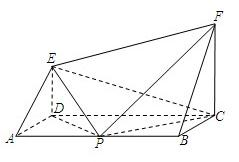 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,P为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,P为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
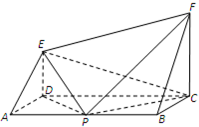 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,DE=a,P为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,DE=a,P为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
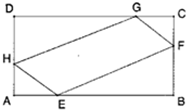 如图,ABCD为矩形草坪,AB=a(m),BC=b(m)(b<a),现要在四边上分别取AE=CF=CG=AH=x(m),将中间部分四边形EFGH建为花坛,记花坛面积为S(m2).
如图,ABCD为矩形草坪,AB=a(m),BC=b(m)(b<a),现要在四边上分别取AE=CF=CG=AH=x(m),将中间部分四边形EFGH建为花坛,记花坛面积为S(m2).查看答案和解析>>
科目:高中数学 来源:2011年江苏省淮安五校高二上学期期末考试数学试卷 题型:解答题
(本题满分14分)
如图, ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC= CF=2a,DE=a, P为AB的中点.

(1)求证:平面PCF⊥平面PDE;
(2)求证:AE∥平面BCF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com