
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据![]() 的面积可求得椭圆中的
的面积可求得椭圆中的![]() ,将点带入椭圆标准方程,结合椭圆中
,将点带入椭圆标准方程,结合椭圆中![]() 的关系即可求得椭圆
的关系即可求得椭圆![]() 的方程;
的方程;
(2)表示出圆的方程,分析斜率存在与不存在两种情况:当斜率不存在时,易知直线与圆相切,可求得切点坐标,当斜率存在时,设出直线方程,由切线性质及点到直线距离公式可求得斜率,进而将直线方程与圆方程联立,求得切点坐标,即可由平面向量数量积的坐标运算求得![]() 的值.
的值.
(1)设椭圆![]() 的焦距为2c,
的焦距为2c,
由![]() 的面积为
的面积为![]() 可得
可得![]() ,
,
![]() ,
,
则![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上可得
上可得![]() ,
,
解之得![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)过原点且斜率不存在的直线显然与圆![]() 相切,切点为
相切,切点为![]() ,
,
当斜率存在时,设过原点![]() 的直线为
的直线为![]() ,即
,即![]() ,
,
由圆心![]() 到直线
到直线![]() 的距离恰好等于圆的半径
的距离恰好等于圆的半径![]() 可得
可得
![]() ,解之得
,解之得![]() ,
,
由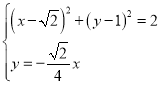 可得
可得![]() ,即
,即![]() ,
,
![]()
![]() ,
,![]() ,即点
,即点![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】随着经济全球化信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
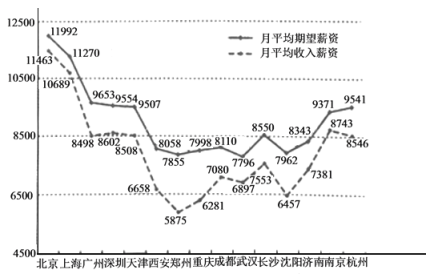
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() ).
).
(1)点![]() 的直角坐标为(2,2),且点
的直角坐标为(2,2),且点![]() 在曲线
在曲线![]() 内,求实数m的取值范围;
内,求实数m的取值范围;
(2)若![]() ,当
,当![]() 变化时,求直线被曲线
变化时,求直线被曲线![]() 截得的弦长的取值范围.
截得的弦长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com