甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为8的事件,求P(A)
(2)现连玩三次,若以B表示甲至少赢两次的事件,C表示乙至少赢一次的事件,则B与C是否为互斥事件,并说明理由.
(3)这种游戏规则公平吗?并说明理由.
解:(1)基本事件有n=5*5=25个.
A中含(3,5),(4,4),(5,3)共m=3种,
∴P(A)=
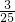
…(4分)
(2)B、C不是互斥事件.
因为他们可以同时发生:甲赢两次的事件,乙赢一次,
故可以同时发生…(6分)
(3)这游戏规则不公平.
若和为偶数的事件D中含:(1,1),(1,3),(1,5),(2,2),
(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),
(5,1),(5,3),(5,5)共13个…(10分)
所以甲赢的概率为

,
乙赢的概率为

,
所以这游戏规则不公平…(12分)
分析:(1)基本事件有n=5*5=25个.A中含(3,5),(4,4),(5,3)共m=3种,由此能求出P(A).
(2)B、C不是互斥事件.因为他们可以同时发生:甲赢两次的事件,乙赢一次,可以同时发生.
(3)这游戏规则不公平.若和为偶数的事件D中含13个基本事件,所以甲赢的概率为

,乙赢的概率为

,所以这游戏规则不公平.
点评:本题考查概率问题在生产实践中的应用,有一定的探索性,对数学思维能力要求较高,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

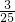 …(4分)
…(4分) ,
, ,
, ,乙赢的概率为
,乙赢的概率为 ,所以这游戏规则不公平.
,所以这游戏规则不公平.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案