
已知函数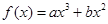 在点
在点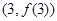 处的切线方程为
处的切线方程为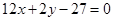 ,且对任意的
,且对任意的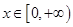 ,
,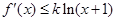 恒成立.
恒成立.
(Ⅰ)求函数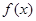 的解析式;
的解析式;
(Ⅱ)求实数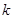 的最小值;
的最小值;
(Ⅲ)求证: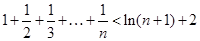 (
(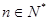 ).
).
(Ⅰ) (Ⅱ)
(Ⅱ)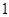
(Ⅲ)先证 ,累加即得.
,累加即得.
【解析】
试题分析:(Ⅰ)将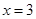 代入直线方程得
代入直线方程得 ,∴
,∴ ①
①
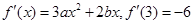 ,∴
,∴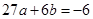 ②
②
联立,解得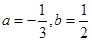 ∴
∴
(Ⅱ) ,∴
,∴ 在
在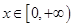 上恒成立;
上恒成立;
即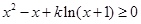 在
在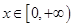 恒成立;
恒成立;
设 ,
, ,
,
∴只需证对于任意的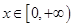 有
有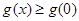
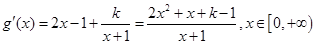
设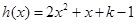 ,
,
1)当 ,即
,即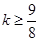 时,
时,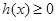 ,∴
,∴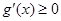
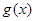 在
在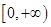 单调递增,∴
单调递增,∴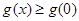
2)当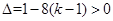 ,即
,即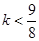 时,设
时,设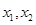 是方程
是方程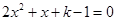 的两根且
的两根且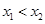
由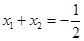 ,可知
,可知 ,分析题意可知当
,分析题意可知当 时对任意
时对任意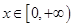 有
有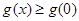 ;
;
∴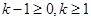 ,∴
,∴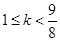
综上分析,实数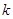 的最小值为
的最小值为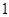 .
.
(Ⅲ)令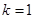 ,有
,有 即
即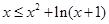 在
在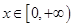 恒成立;
恒成立;
令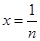 ,得
,得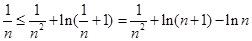
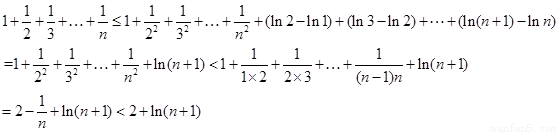
∴原不等式得证.
考点:利用导数研究曲线上某点切线方程;函数解析式的求解及常用方法;不等式的证明.
点评:本题考查了利用导数研究函数的切线方程问题,在曲线上某点处的切线的斜率就是该点的导数值,考查了导数在最大值和最小值中的应用,体现了数学转化思想和分类讨论的数学思想.特别是(Ⅲ)的证明,用到了放缩法和裂项相消,此题属难度较大的题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届辽宁省五校协作体届高三摸底考试理科数学试卷(解析版) 题型:解答题
已知函数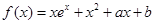 在点
在点 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+ )均有
)均有 恒成立.
恒成立.
(Ⅰ)求a,b,c的值;
(Ⅱ)求证: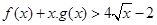 .
.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知函数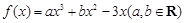 在点
在点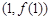 处的切线方程为
处的切线方程为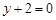 .
.
(1)求函数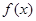 的解析式;
的解析式;
(2)若经过点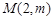 可以作出曲线
可以作出曲线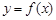 的三条切线,求实数
的三条切线,求实数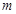 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届江西省南昌市高二2月份月考文科数学试卷(解析版) 题型:解答题
(本小题13分)已知函数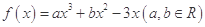 在点
在点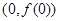 处的切线与直线
处的切线与直线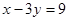 垂直.
垂直.
(1)若对于区间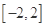 上任意两个自变量的值
上任意两个自变量的值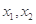 都有
都有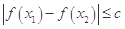 ,求实数
,求实数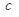 的最小值;
的最小值;
(2)若过点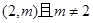 可作曲线
可作曲线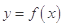 的三条切线,求实数
的三条切线,求实数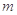 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏南四校高三12月月考试数学试卷(解析版) 题型:解答题
已知函数 在点
在点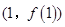 处的切线方程为
处的切线方程为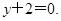
(1)求函数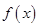 的解析式;
的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值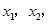 都有
都有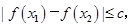 求实数c的最小值.
求实数c的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com