7
分析:把所给的式子化为 8
n-1,展开得 9
n+(-1)
1•

+…+(-1)
n-1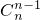
9+(-1)
n-1,分析结构特征可得式子被9除所得的余数.
解答:∵
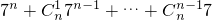
=
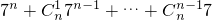
+1-1=(7+1)
n-1=8
n-1
=(9-1)
n-1=9
n+(-1)
1•

+…+(-1)
n-1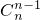
9+(-1)
n-1.
显然,式子中,除了最后两项(-1)
n-1以外,其余的各项都能被9整除.
而由n为正奇数可得 (-1)
n-1=-2,
故所给的式子被9除所得的余数为7,
故答案为 7.
点评:本题主要考查二项式定理的应用,把所给的式子化为 9
n+(-1)
1•

+…+(-1)
n-1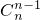
9+(-1)
n-1,是解题的关键,属于中档题.

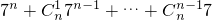 被9除所得的余数为:________.
被9除所得的余数为:________.