练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆，过点作的异于轴的切线，过点作的异于轴的切线.设与交于点，记的轨迹为.

    （1）求的方程；

    （2）已知，在点处的切线交直线于点，过原点与平行的直线交于点.证明：以为直径的圆截轴的弦长为定值.

    【答案】（1）（2）证明见解析

    【解析】

    （1）由切线长定理结合题意得，由椭圆性质可得点的轨迹是以，为焦点，长轴长为4的椭圆，即可得解；

    （2）设直线，，联立方程可得点，进而可得直线的方程为，求得点、的坐标后，再求圆的方程即可得解.

    （1）

    如图，设两直线与圆的切点分别为M、N，设圆与x轴的交点为Q，

    由切线长定理得，，，

    所以，

    所以点的轨迹是以，为焦点，长轴长为4的椭圆，

    所以，，所以，

    所以的轨迹方程是.

    （2）设直线，，

    将代入得

    ，

    ，化简得.

    ，

    ，所以，

    从而，

    所以直线的方程为，

    令得，所以.

    易得，

    所以以为直径的圆是，

    令得，

    所以以为直径的圆截轴所得的弦长为4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】到2020年，我国将全面建立起新的高考制度，新高考采用模式，其中语文、数学、英语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣、爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门（6选3）参加考试，满分各100分.为了顺利迎接新高考改革，某学校采用分层抽样的方法从高一年级1000名（其中男生550名，女生450名）学生中抽取了名学生进行调查.

    （1）已知抽取的名学生中有女生45名，求的值及抽取的男生的人数.

    （2）该校计划在高一上学期开设选修中的“物理”和“地理”两个科目，为了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目，且只能选择一个科目），得到如下列联表.

    选择“物理”

    选择“地理”

    总计

    男生

    10

    女生

    25

    总计

    （i）请将列联表补充完整，并判断是否有以上的把握认为选择科目与性别有关系.

    （ii）在抽取的选择“地理”的学生中按性别分层抽样抽取6名，再从这6名学生中抽取2名，求这2名中至少有1名男生的概率.

    附：，其中.

    0.05

    0.01

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中,曲线C的参数方程为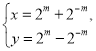(m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθρsinθ2=0.

    (1)求C和l的直角坐标方程;

    (2)设直线l与曲线C的公共点为P,Q,求|PQ|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱柱的所有棱长都为2，且.

    （1）证明：平面平面；

    （2）求直线与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】坐标系与参数方程：在平面直角坐标系中，以原点为极点，轴的非负半轴为极轴建立极坐标系，已知点的极坐标为，直线的极坐标方程为，且点在直线上

    （Ⅰ）求的值和直线的直角坐标方程及的参数方程；

    （Ⅱ）已知曲线的参数方程为，（为参数），直线与交于两点，求的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】天干地支，简称为干支，源自中国远古时代对天象的观测.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”称为十天干，“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”称为十二地支.干支纪年法是天干和地支依次按固定的顺序相互配合组成，以此往复，60年为一个轮回.现从农历2000年至2019年共20个年份中任取2个年份，则这2个年份的天干或地支相同的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

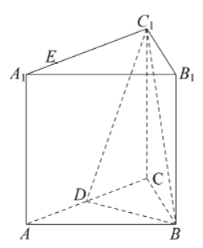
    【题目】如图，正三棱柱的所有棱长都为，是的中点，在边上，.

    （1）证明：平面平面；

    （2）若是侧面内的动点，且平面.

    ①在答题卡中作出点的轨迹，并说明轨迹的形状（不需要说明理由）；

    ②求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场一年中各月份的收入、支出情况的统计如图所示，下列说法中正确的是______.

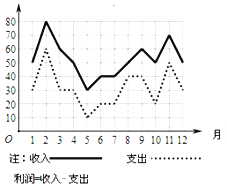
    ①2至3月份的收入的变化率与11至12月份的收入的变化率相同；

    ②支出最高值与支出最低值的比是6:1；

    ③第三季度平均收入为50万元；

    ④利润最高的月份是2月份。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】渭南市公安局交警支队依据《中华人民共和国道路交通安全法》第条规定：渭南城区所有主干道路凡机动车途经十字口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人.违反者将被处以元罚款，记分的行政处罚.下表是渭南市一主干路段，监控设备所抓拍的个月内，机动车驾驶员不“礼让斑马线”行为统计数据：

    月份

    违章驾驶员人数

    （1）请利用所给数据求违章人数与月份之间的回归直线方程；

    （2）预测该路月份的不“礼让斑马线”违章驾驶员人数；

    （3）若从表中、月份分别抽取人和人，然后再从中任选人进行交规调查，求拍到的两人恰好来自同一月份的概率.

    参考公式：，.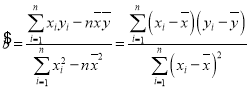

    查看答案和解析>>

    同步练习册答案