在△ABC中,已知a
2-a=2(b+c),a+2b=2c-3,
(1)若sinC:sinA=4:
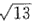
,求a,b,c;
(2)求△ABC的最大角的弧度数。
解:(1)由正弦定理,得

,
∴可设c=4k,

,
由已知条件,得a
2-a-2c=2b,2c-a-3=2b,
故a
2-a-2c=2c-a-3,
∴

,
即13k
2-16k+3=0,解得

或k=1,
当

时,b<0,故舍去,
∴k=1,∴

。
(2)由已知的两个式子消去2b,得

,
代入a
2-a-2b-2c=0中,得


(a-3)(a+1),
∵a,b,c>0,
所以a>3,
又

,

,
∴b<c,a<c,故c为最大边,所以∠C最大,
∵


,
而0<C<π,∴

。
故△ABC的最大角为角C,弧度数为

。
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
在△ABC中,已知A、B、C成等差数列,求tg(
)+
tg(
)tg(
)+tg(
)的值.
查看答案和解析>>
科目:高中数学
来源:
题型:
在△ABC中,已知A=45°,a=2,b=
,则B等于( )
查看答案和解析>>
科目:高中数学
来源:
题型:
在△ABC中,已知a=
,b=
,1+2cos(B+C)=0,求:
(1)角A,B;
(2)求BC边上的高.
查看答案和解析>>
科目:高中数学
来源:
题型:
在△ABC中,已知A=60°,
•=1,则△ABC的面积为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
在△ABC中,已知a=1,b=2,
cosC=.
(1)求AB的长;
(2)求sinA的值.
查看答案和解析>>

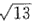 ,求a,b,c;
,求a,b,c;