
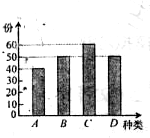
 (2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示:
(2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示:| 满意 | 一般 | 不满意 | |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
| 20 |
| 200 |
| 20 |
| 200 |
| 20 |
| 200 |
| 20 |
| 200 |
| 5 |
| 6 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
 (2012•枣庄一模)如图,CDEF是以圆O为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在扇形OCFH内”(点H将劣弧
(2012•枣庄一模)如图,CDEF是以圆O为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在扇形OCFH内”(点H将劣弧 |
| EF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•枣庄一模)给定两个长度为1的平面向量
(2012•枣庄一模)给定两个长度为1的平面向量| OA |
| OB |
 |
| AB |
| OC |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| b |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com