
【题目】如图,在四棱锥S﹣ABCD中,SA⊥底面ABCD,底面ABCD是平行四边形,E是线段SD上一点.
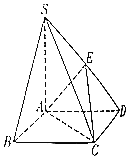
(1)若E是SD的中点,求证:SB∥平面ACE;
(2)若SA=AB=AD=2,SC=2![]() ,且DE
,且DE![]() DS,求二面角S﹣AC﹣E的余弦值.
DS,求二面角S﹣AC﹣E的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意连结BD,交AC于点O,连结OE,可证OE∥SB,SB∥平面ACE得证;
(2)建立空间直角坐标系,求得平面SAC与平面ACE的法向量,代入公式求二面角的余弦值即可.
(1)证明:连结BD,交AC于点O,连结OE,
∵底面ABCD是平行四边形,∴O是BD的中点,
∵E是SD的中点,∴OE∥SB,
∵SB平面ACE,OE平面ACE,
∴SB∥平面ACE.
(2)∵SA⊥底面ABCD,AC平面ABCD,
∴SA⊥AC,
在Rt△SAC中,SA=2,SC=2![]() ,
,
∴AC=2,
∵AB=AD=2,
∴△ABC,△ACD都是等边三角形,
∴BD=2![]() ,
,
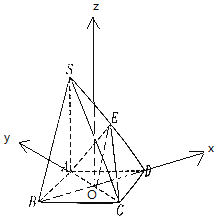
以O为原点,OD为x轴,OA为y轴,过O作AS的平行线为z轴,建立空间直角坐标系,
O(0,0,0),D(![]() ,0,0),A(0,1,0),S(0,1,2),
,0,0),A(0,1,0),S(0,1,2),
![]() (
(![]() ,1,2),
,1,2),![]() (
(![]() ,
,![]() ),
),
![]() (
(![]() ),
),
∵BD⊥平面SAC,取平面SAC的一个法向量![]() (
(![]() ),
),
设平面ACE的法向量![]() (x,y,z),
(x,y,z),
则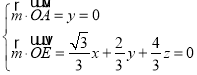 ,取x=4,得
,取x=4,得![]() (4,0,
(4,0,![]() ),
),
设二面角S﹣AC﹣E的平面角为θ,
则cosθ .
.
∴二面角S﹣AC﹣E的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为了了解公司800名员工对公司食堂组建的需求程度,将这些员工编号为1,2,3,…,800,对这些员工使用系统抽样的方法等距抽取100人征求意见,有下述三个结论:①若25号员工被抽到,则105号员工也会被抽到;②若32号员工被抽到,则1到100号的员工中被抽取了10人;③若88号员工未被抽到,则10号员工一定未被抽到;其中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com