
【题目】已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.
(1)求点M的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.
【答案】
(1)解:由题意坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5,
得 ![]() =5.
=5. ![]() ,化简得x2+y2﹣2x﹣2y﹣23=0.
,化简得x2+y2﹣2x﹣2y﹣23=0.
即(x﹣1)2+(y﹣1)2=25.
∴点M的轨迹方程是(x﹣1)2+(y﹣1)2=25,
所求轨迹是以(1,1)为圆心,以5为半径的圆
(2)解:当直线l的斜率不存在时,过点A(﹣2,3)的直线l:x=﹣2,
此时过点A(﹣2,3)的直线l被圆所截得的线段的长为:2 ![]() =8,
=8,
∴l:x=﹣2符合题意.
当直线l的斜率存在时,设过点A(﹣2,3)的直线l的方程为y﹣3=k(x+2),即kx﹣y+2k+3=0,
圆心到l的距离d= ![]() ,
,
由题意,得 ![]() +42=52,解得k=
+42=52,解得k= ![]() .∴直线l的方程为
.∴直线l的方程为 ![]() x﹣y+
x﹣y+ ![]() =0.即5x﹣12y+46=0.
=0.即5x﹣12y+46=0.
综上,直线l的方程为x=﹣2,或5x﹣12y+46=0
【解析】(1)直接利用距离的比,列出方程即可求点M的轨迹方程,然后说明轨迹是什么图形;(2)设出直线方程,利用圆心到直线的距离,半径与半弦长满足的勾股定理,求出直线l的方程.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: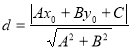 .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinxcosx﹣ ![]() acos2x+
acos2x+ ![]() a+b(a>0)
a+b(a>0)
(1)写出函数的单调递减区间;
(2)设x∈[0, ![]() ],f(x)的最小值是﹣2,最大值是
],f(x)的最小值是﹣2,最大值是 ![]() ,求实数a,b的值.
,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a2= ![]() ,且an+1=3an﹣1(n∈N*).
,且an+1=3an﹣1(n∈N*).
(1)求数列{an}的通项公式以及数列{an}的前n项和Sn的表达式;
(2)若不等式 ![]() ≤m对n∈N*恒成立,求实数m的取值范围.
≤m对n∈N*恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,an+1=4an﹣3n+1,n∈N*(Ⅰ)证明:数列{an﹣n}是等比数列
(Ⅱ)记数列{an}的前n项和为Sn , 求证:Sn+1≤4Sn , 对任意n∈N*成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
A.![]()
B.10a
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA﹣csinC=(a﹣b)sinB.
(1)求角C的大小;
(2)若边长 ![]() ,求△ABC的周长最大值.
,求△ABC的周长最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则16分钟后P点距地面的高度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的 ![]() 是较小的两份之和,问最小一份为( )
是较小的两份之和,问最小一份为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,点M在AB上,且AM:MB=1:2,E为PB的中点. 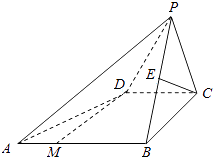
(1)求证:CE∥平面ADP;
(2)求证:平面PAD⊥平面PAB;
(3)棱AP上是否存在一点N,使得平面DMN⊥平面ABCD,若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com