
【题目】已知二次函数![]() .
.
(1)若方程![]() 两个根之和为4,两根之积为3,且过点(2,-1).求
两个根之和为4,两根之积为3,且过点(2,-1).求![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(ⅰ)求解关于![]() 的不等式
的不等式![]()
(ⅱ)设函数![]() ,求函数
,求函数![]() 的最大值
的最大值
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 是边长等于2的等边三角形,四边形
是边长等于2的等边三角形,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的点,
上的点,![]() .
.![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
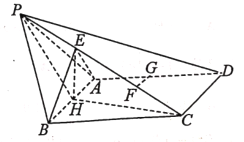
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
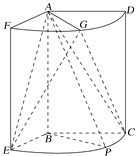
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.
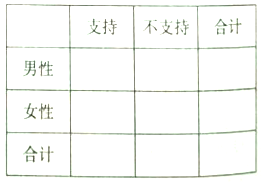
(Ⅰ)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附: 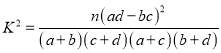 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为抛物线
为抛物线![]() 上的两点,
上的两点,![]() 与
与![]() 的中点的纵坐标为4,直线
的中点的纵坐标为4,直线![]() 的斜率为
的斜率为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() 、
、![]() 为抛物线
为抛物线![]() (除原点外)上的不同两点,直线
(除原点外)上的不同两点,直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且满足
,且满足![]() ,记抛物线
,记抛物线![]() 在
在![]() 、
、![]() 处的切线交于点
处的切线交于点![]() ,若点
,若点![]() 、
、![]() 的中点的纵坐标为8,求点
的中点的纵坐标为8,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条线段围成.设圆弧
的两条线段围成.设圆弧![]() 、
、![]() 所在圆的半径分别为
所在圆的半径分别为![]() 、
、![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).

(1)若![]() ,
,![]() ,
,![]() ,求花坛的面积;
,求花坛的面积;
(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为![]() 元/米,弧线部分的装饰费用为
元/米,弧线部分的装饰费用为![]() 元/米,预算费用总计
元/米,预算费用总计![]() 元,问线段
元,问线段![]() 的长度为多少时,花坛的面积最大?
的长度为多少时,花坛的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com