观察由奇数组成的数阵,若第k行有2k-1个数,第k行的第s个数(从左数起)记为(k,s),则2009记为________
1
3 5 7
9 11 13 15 17
19 21 23 25 27 29 31
…
(32,44)
分析:根据第k行有2k-1个数知每行数的个数成等差数列,为了探求2009位于什么位置,先求(k,s),就必须求出前k-1行一共出现了多少个数,根据等差数列求和公式可求,进一步分析可知答案.
解答:由于2009=1+(1005-1)×2,
故2009位于奇数列的第1005项,
又由奇数组成的数阵前31行共有奇数1+3+5+…+(2×31-1)=961个数,
前32行共有奇数1+3+5+…+(2×32-1)=1024个数,
故2009应位于第32行,
又第32行的第一个数为1+(962-1)×2=1923,
且第32构成一个等差数列,故2009位于其第
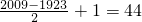
项,
则2009记为 (32,44).
故答案为:(32,44).
点评:考查数列的性质和应用,解题是注意公式的灵活应用,此题是以一个数阵形式呈现的,考查观察、分析、归纳、解决问题的能力,属中档题.

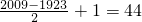 项,
项,

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案