
【题目】某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
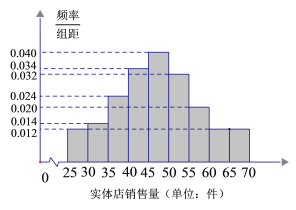
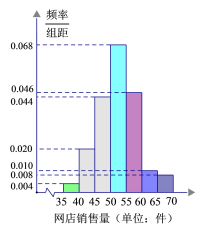
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50件的概率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1200元,每售出一件利润为50元,求该门市一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量中位数的估计值(精确到0.01).
【答案】(1)80;(2)0.38;(3)![]()
【解析】
(1)由频率分布直方图即可得到过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2) 由题意,设该门市一天售出![]() 件,则
件,则![]() ,设该门市一天获利不低于800元为事件
,设该门市一天获利不低于800元为事件![]() ,则
,则![]() ,从而得到结果;
,从而得到结果;
(3)利用频率分布直方图估计该服装店网店销售量中位数.
(1)由题意,网店销量都不低于50件共有![]() (天),实体店销售量不低于50件的天数为
(天),实体店销售量不低于50件的天数为![]() (天),实体店和网店销售量都不低于50件的天数为
(天),实体店和网店销售量都不低于50件的天数为![]() (天),
(天),
故实体店和网店至少有一边销售量不低于50的天数为![]() (天)
(天)
(2)由题意,设该门市一天售出![]() 件,则获利为
件,则获利为![]() .
.
设该门市一天获利不低于800元为事件![]() ,则
,则
![]() .
.
故该门市 一天获利不低于800元的概率为0.38..
(3)因为网店销售量频率分布直方图中,销售量低于![]() 的直方图面积为
的直方图面积为
![]() ,
,
销售量低于![]() 的直方图面积为
的直方图面积为![]()
故网店销售量的中位数的估计值为![]() (件)
(件)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最未打的数学家之一,他所著的《四元玉鉴》卷中“如像招数一五间”,有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日?”.其大意为:“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,修筑堤坝的每人每天发大米3升,共发出大米40392升,问修筑堤坝多少天”.在这个问题中,前5天应发大米( )
A. 894升 B. 1170升 C. 1275升 D. 1457升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生将语文、数学、英语、物理、化学、生物6科的作业安排在周六、周日完成,要求每天至少完成两科,且数学,物理作业不在同一天完成,则完成作业的不同顺序种数为( )
A. 600B. 812C. 1200D. 1632
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区共100名观众,得到如下的
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区共100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
A | 30 | y | |
B | x | z | |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35,且
地区当中“非常满意”的观众的概率为0.35,且![]() .请完成上述表格,并根据表格判断是否有95%的把握认为观众的满意程度与所在地区有关系?
.请完成上述表格,并根据表格判断是否有95%的把握认为观众的满意程度与所在地区有关系?
附:参考公式:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当生物死亡后,它机体内原有的碳14会按确定的规律衰减.按照惯例,人们将每克组织的碳14含量作为一个单位大约每经过5730年,一个单位的碳14衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了_____个“半衰期”.(提示:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是
分别是![]() 的中点,点
的中点,点![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱锥![]() 的体积分别为
的体积分别为![]() ,当
,当![]() 为何值时,
为何值时, ![]() 最大?最大值为多少?
最大?最大值为多少?
(Ⅱ)若![]() 平面
平面![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
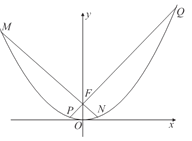
【题目】已知F为抛物线E:![]() (p>0)的焦点,C(
(p>0)的焦点,C(![]() ,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线
,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
(1)求抛物线E的方程及点C的坐标;
(2)试问![]() 是否为定值?若是,求出此定值;若不是,请说明理由;
是否为定值?若是,求出此定值;若不是,请说明理由;
(3)证明直线AB经过一个定点,求此定点的坐标,并求△AOB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯将于2019年8月31日至9月15日在中国北京、广州等八座城市举行.届时,甲、乙、丙、丁四名篮球世界杯志愿者将随机分到![]() 、
、![]() 、
、![]() 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人不在同一个岗位服务的概率;
(2)设随机变量![]() 为这四名志愿者中参加
为这四名志愿者中参加![]() 岗位服务的人数,求
岗位服务的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com