
椭圆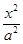 +
+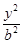 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=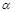 , 且
, 且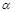 ∈[
∈[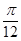 ,
,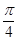 ], 则该椭圆离心率的取值范围为 (
)
], 则该椭圆离心率的取值范围为 (
)
A.[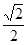 ,1 ) B.[
,1 ) B.[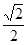 ,
,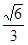 ] C.[
] C.[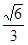 , 1) D.[
, 1) D.[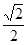 ,
,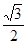
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:选择题
如图所示,已知A,B分别为椭圆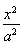 +
+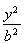 =1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
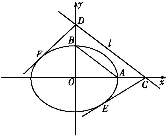
(A)±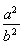 (B)±
(B)±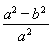
(C)±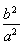 (D)±
(D)±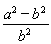
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
设椭圆 +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y- )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源:2013届陕西省高二上学期期中文科数学试卷 题型:选择题
已知双曲线 -
- =1和椭圆
=1和椭圆 +
+ =1(a>0,m>b>0)的离心率互为倒数,那么以a、b、
=1(a>0,m>b>0)的离心率互为倒数,那么以a、b、 为边长的三角形是( )
为边长的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角或钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com