
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
(1);(2);(3)见解析.
解析试题分析:(1)先记“甲以4比1获胜”为事件A,由题意甲乙一共比赛5局,则甲前4局比赛中有且只有3局获胜,第5局比赛一定获胜,易得甲以4比1获胜的概率为P(A)=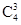 ()3·()4-3·=;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.
()3·()4-3·=;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.
试题解析:(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是. 1分
记“甲以4比1获胜”为事件A,则P(A)=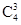 ()3·()4-3·=. 3分
()3·()4-3·=. 3分
(2)记“乙获胜且比赛局数多于5局”为事件B.
因为乙以4比2获胜的概率为P1=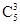
 ·
· ·=,
·=,
乙以4比3获胜的概率为P2= ·
·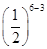 ·=,
·=,
所以P(B)=P1+P2=. 7分
(3)设比赛的局数位X,则X的可能取值为4,5,6,7. 8分 ,
, ,
,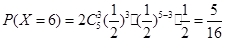 ,
, , 11分
, 11分
比赛局数的分布列为
考点:1、概率;2、概率分布列.X 4 5 6 7 P 




科目:高中数学 来源: 题型:解答题
甲有一只放有x个红球,y个黄球,z个白球的箱子,乙有一只放有3个红球,2个黄球,1个白球的箱子,
(1)两个各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜。若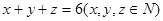 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;
2)在(1)下又规定当甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时x、y、z的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程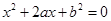 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A,B,C,D四个城市,它们各自有一个著名的旅游点,依次记为A,b,C,D,把A,B,C,D和A,b,C,D分别写成左、右两列.现在一名旅游爱好者随机用4条线把城市与旅游点全部连接起来, 构成“一一对应”.规定某城市与自身的旅游点相连称为“连对”,否则称为“连错”,连对一条得2分,连错一条得0分.
(Ⅰ)求该旅游爱好者得2分的概率.
(Ⅱ)求所得分数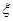 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为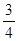 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为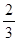 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分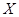 的分布列及数学期望
的分布列及数学期望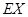 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组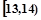 ;第二组
;第二组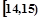 ,……,第五组
,……,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 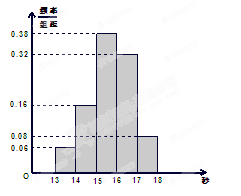
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设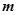 、
、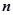 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知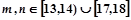 ,求事件“
,求事件“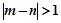 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为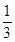 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为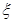 ,求
,求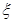 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
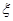 的分布列及其期望.
的分布列及其期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
(I)求该班学生参加活动的人均次数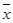 ;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率
;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率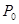 .
.
(III)从该班中任选两名学生,用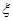 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量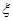 的分布列及数学期望
的分布列及数学期望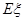 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com