
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() .M为CD的中点.
.M为CD的中点.

(1)若点E为PC的中点,求证:BE∥平面PAD;
(2)当平面PBD⊥平面ABCD时,求点A到平面CEM的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连结EM,BM,可证明![]() 都平行于平面
都平行于平面![]() ,从而得平面
,从而得平面![]() ,因此得证BE∥平面PAD;
,因此得证BE∥平面PAD;
(2)点A到平面CME的距离即点A到平面PCD的距离,设为h,连结AC,交BD于点O,连结PO,可证得![]() 平面
平面![]() ,则利用
,则利用![]() 可求得
可求得![]() .
.
证明:(1)连结EM,BM.由已知得,![]() 为等边三角形,
为等边三角形,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
又∵![]() ,
,![]() ,∴
,∴![]() .
.
∵E为PC的中点,M为CD的中点,∴![]() .又∵
.又∵![]() ,
,![]() ,∴
,∴![]() .∵
.∵![]() ,∴平面
,∴平面![]() .
.
∵![]() ,∴
,∴![]() .
.
(2)连结AC,交BD于点O,连结PO,
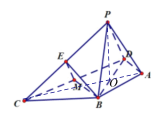
由对称性知,O为BD的中点,且![]() ,
,![]() ,∵
,∵![]() ,且交线为BD,
,且交线为BD,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
在![]() 中,
中,![]() .
.
则![]() ,∴
,∴![]() ,
,
由题意点A到平面CME的距离即点A到平面PCD的距离,设为h,则有
![]() 得
得![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把以上这段文字写成公式,即![]() .已知
.已知![]() 满足
满足![]()
![]() .且
.且![]() ,则用以上给出的公式可求得
,则用以上给出的公式可求得![]() 的面积为____.
的面积为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】即将于![]() 年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到
年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到![]() 年到
年到![]() 年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年份 |
|
|
|
|
|
|
|
|
|
|
序号 |
|
|
|
|
|
|
|
|
|
|
年平均工资 |
|
|
|
|
|
|
|
|
|
|
(1)请根据上表的数据,利用线性回归模型拟合思想,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 的计算结果根据四舍五入精确到小数点后第二位);
的计算结果根据四舍五入精确到小数点后第二位);
(2)如果毕业生对年平均工资的期望值为8.5万元,请利用(1)的结论,预测![]() 年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断
年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断![]() 年平均工资能否达到他的期望.
年平均工资能否达到他的期望.
参考数据:![]() ,
,![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附:对于一组具有线性相关的数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为

 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
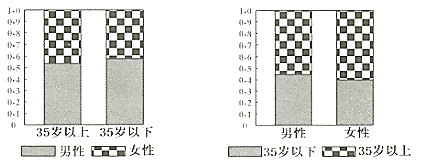
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽奖活动中,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
(1)求![]() 能获一等奖的概率;
能获一等奖的概率;
(2)若![]() ,
,![]() 已获一等奖,求
已获一等奖,求![]() 能获奖的概率.
能获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的两动点,且以
上的两动点,且以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点的凸四边形的面积的最大值为
四个点为顶点的凸四边形的面积的最大值为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 经过点
经过点![]() ,且直线
,且直线![]() 的斜率是直线
的斜率是直线![]() ,
,![]() 的斜率的等比中项,求
的斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形![]() 中,
中,![]() 等边三角形,
等边三角形,![]() ,以
,以![]() 为折痕将
为折痕将![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
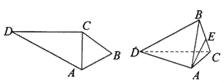
(1)设![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com