
【题目】已知动点![]() 是圆
是圆![]() :
: ![]() 上的任意一点,点
上的任意一点,点![]() 与点
与点![]() 的连线段的垂直平分线和
的连线段的垂直平分线和![]() 相交于点
相交于点![]() .
.
(I)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(II)过坐标原点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于点
于点![]() ,
, ![]() 两点,直线
两点,直线![]() 与坐标轴不重合.
与坐标轴不重合. ![]() 是轨迹
是轨迹![]() 上的一点,若
上的一点,若![]() 的面积是4,试问直线
的面积是4,试问直线![]() ,
, ![]() 的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线![]() 的参数方程为
的参数方程为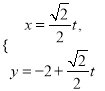 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为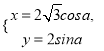 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和
和![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若![]() 为曲线
为曲线![]() 上的一个动点,求
上的一个动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】借助计算器填写下表:
|
|
|
|
|
0 | ||||
1 | ||||
10 | ||||
20 | ||||
30 | ||||
50 | ||||
70 | ||||
100 | ||||
150 | ||||
200 | ||||
250 | ||||
300 |
观察表中的变化并归纳各函数递增的规律:
(1)一次函数![]() 与幂函数
与幂函数![]() 之间比较得出的规律;
之间比较得出的规律;
(2)幂函数![]() 与指数函数
与指数函数![]() 之间比较得出的规律;
之间比较得出的规律;
(3)指数函数![]() 与
与![]() 之间比较得出的规律.
之间比较得出的规律.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数) .
为实常数) .
(I)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值及相应的
上的最大值及相应的![]() 值;
值;
(II)当![]() 时,讨论方程
时,讨论方程![]() 根的个数.
根的个数.
(III)若![]() ,且对任意的
,且对任意的![]() ,都有
,都有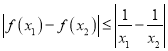 ,求
,求
实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地居民用水采用阶梯水价,其标准为:每户每月用水量不超过15吨的部分,每吨3元;超过15吨但不超过25吨的部分,每吨4.5元;超过25吨的部分,每吨6元.
(1)求某户居民每月需交水费![]() (元)关于用水量
(元)关于用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)若![]() 户居民某月交水费67.5元,求
户居民某月交水费67.5元,求![]() 户居民该月的用水量.
户居民该月的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣cos2x﹣2![]() sinxcosx(x∈R).
sinxcosx(x∈R).
(1)求f(x)的单调递增区间;
(2)求函数f(x)在区间[![]() ,
,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com