
在平面直角坐标系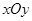 中,
中,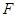 是抛物线
是抛物线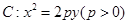 的焦点,
的焦点,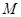 是抛物线
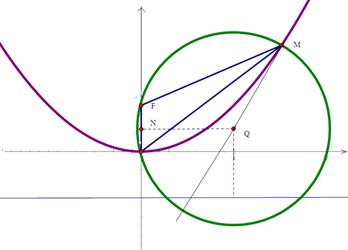
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过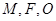 三点的圆的圆心为
三点的圆的圆心为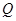 ,点
,点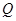 到抛物线
到抛物线 的准线的距离为
的准线的距离为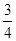 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)是否存在点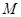 ,使得直线
,使得直线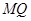 与抛物线
与抛物线 相切于点
相切于点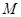 ?若存在,求出点
?若存在,求出点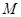 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)若点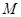 的横坐标为
的横坐标为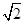 ,直线
,直线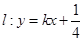 与抛物线
与抛物线 有两个不同的交点
有两个不同的交点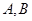 ,
,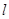 与圆
与圆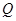 有两个不同的交点
有两个不同的交点 ,求当
,求当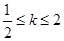 时,
时,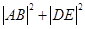 的最小值.
的最小值.
: (Ⅰ)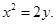
(Ⅱ)存在,点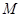 的坐标为
的坐标为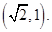
(Ⅲ)当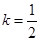 时,
时,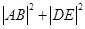 的最小值为
的最小值为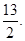
【解析】:(Ⅰ)
如图,取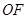 的中点
的中点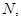 则
则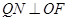 ,即
,即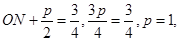
所以抛物线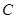 的方程为
的方程为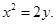
(Ⅱ)
设存在点 使得直线
使得直线 与抛物线
与抛物线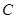 相切于点
相切于点
由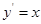 得切线
得切线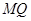 的斜率为
的斜率为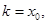 直线
直线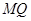 的方程为
的方程为
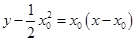 ,代入
,代入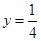 得
得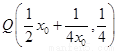 ,
,
由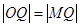 得
得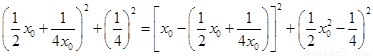 ,
,
化简得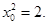
因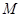 是抛物线
是抛物线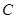 上位于第一象限内的点,所以
上位于第一象限内的点,所以
所以所求的点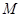 的坐标为
的坐标为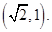
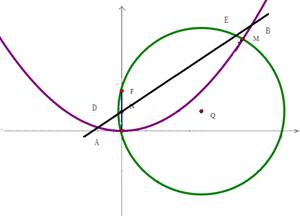
(Ⅲ)由(Ⅱ)可知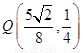 ,
,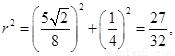
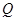 到直线
到直线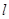 的距离的平方为
的距离的平方为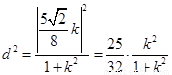 ,
,
所以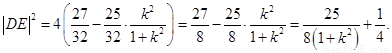 .
.
联立 得
得
所以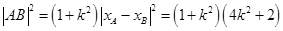 ,
,
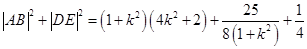 ,
,
令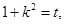 由于
由于 ,所以
,所以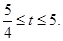
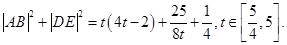
设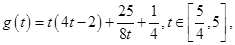
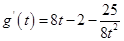 .
.
当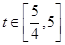 时,
时,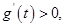
 为增函数,
为增函数,
所以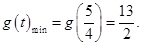
即当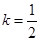 时,
时,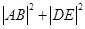 的最小值为
的最小值为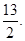
【考点定位】本题通过抛物线和圆的性质确定抛物线方程,呈现出对基础知识的考查。并进一步把问题深化,考查了切线方程的求法,点到直线的距离公式,曲线的弦长运算等,最后通过导数工具求得结果,有很强的综合性,着力体现了能力考查


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com