
分析 $\overrightarrow{AI}=m\overrightarrow{BI}+n\overrightarrow{CI}$=m$\overrightarrow{AI}+n\overrightarrow{AI}-m\overrightarrow{AB}-n\overrightarrow{AC}$,从而(m+n-1)•$\frac{5\sqrt{3}}{2}|\overrightarrow{AI}|$=25m+20n,再由$(m+n-1)•4\sqrt{3}|\overrightarrow{AI}|=20m+64n$,得到5m=8n,由此能求出7(|m|+|n|)的值.
解答 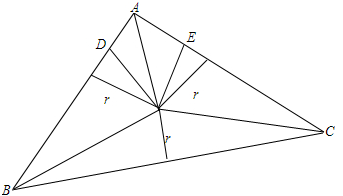 解:∵△ABC中,AB=5,AC=8.∠BAC=60°,I为△ABC内心,
解:∵△ABC中,AB=5,AC=8.∠BAC=60°,I为△ABC内心,
满足$\overrightarrow{AI}$=m$\overrightarrow{BI}$+n$\overrightarrow{CI}$,
∴$\overrightarrow{AI}=m\overrightarrow{BI}+n\overrightarrow{CI}$=m($\overrightarrow{AI}-\overrightarrow{AB}$)+n($\overrightarrow{AI}-\overrightarrow{AC}$)=m$\overrightarrow{AI}+n\overrightarrow{AI}-m\overrightarrow{AB}-n\overrightarrow{AC}$,
∴$m\overrightarrow{AB}+n\overrightarrow{AC}=(m+n-1)\overrightarrow{AI}$,∴(m+n-1)$\overrightarrow{AI}•\overrightarrow{AB}$=m${\overrightarrow{AB}}^{2}+n•\overrightarrow{AB}•\overrightarrow{AC}$,
∴(m+n-1)|$\overrightarrow{AI}$|×$5×\frac{\sqrt{3}}{2}$=m×25+n×5×$8×\frac{1}{2}$,
即(m+n-1)•$\frac{5\sqrt{3}}{2}|\overrightarrow{AI}|$=25m+20n,①
又(m+n-1)$\overrightarrow{AI}•\overrightarrow{AC}$=m$\overrightarrow{AB}•\overrightarrow{AC}$+n${\overrightarrow{AC}}^{2}$,
(m+n-1)•|$\overrightarrow{AI}$|$•8•\frac{\sqrt{3}}{2}$=m×$5×8×\frac{1}{2}$+64n,
∴$(m+n-1)•4\sqrt{3}|\overrightarrow{AI}|=20m+64n$,②
$\frac{①}{②}$,得5m=8n,③
又$\overrightarrow{AI}$=$\frac{m}{m+n-1}$$\overrightarrow{AB}+\frac{n}{m+n-1}\overrightarrow{AC}$,∴AEID为菱形,
∴|$\frac{m\overrightarrow{AB}}{m+n-1}$|=|$\frac{n\overrightarrow{AC}}{m+n-1}$|,
∴m|$\overrightarrow{AB}$|=n|$\overrightarrow{AC}$|,∴5m=8n,
又|$\overrightarrow{BC}$|2=52+82-2×$5×8×\frac{1}{2}$=49,∴|BC|=7,
${S}_{△ABC}=\frac{1}{2}×5×8×\frac{\sqrt{3}}{2}=10\sqrt{3}$,r=$\sqrt{3}$∴|$\overrightarrow{AI}$|=2$\sqrt{3}$,
代入②中,(m+n-1)×6=5m+16n,即m-10n=6,④
③④联立,解得m=-$\frac{48}{42}$,n=-$\frac{30}{42}$,
∴7(|m|+|n|)=13.
故答案为:13.
点评 本题考查代数式的值的求法,是中档题,解题时要认真审题,注意三角形内心性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2mS2n≥Sm+n2,lnS2mlnS2n≤ln2Sm+n | |
| B. | S2mS2n≤Sm+n2,lnS2mlnS2n≤ln2Sm+n | |
| C. | S2mS2n≥Sm+n2,lnS2mlnS2n≥ln2Sm+n | |
| D. | S2mS2n≤Sm+n2,lnS2mlnS2n≥ln2Sm+n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com