
【题目】已知p:x2﹣7x+10<0,q:x2﹣4mx+3m2<0,其中m>0.
(1)若m=4,且p∧q为真,求x的取值范围;
(2)若¬q是¬p的充分不必要条件,求实数m的取值范围.
【答案】
(1)解:由x2﹣7x+10<0,解得2<x<5,所以p:2<x<5;
又x2﹣4mx+3m2<0,因为m>0,解得m<x<3m,所以q:m<x<3m.
当m=4时,q:4<x<12,又p∧q为真,p,q都为真,所以4<x<5
(2)解:由q是p的充分不必要条件,即qp,p≠>q,
其逆否命题为pq,q≠>p,
由(1)p:2<x<5,q:m<x<3m,
所以 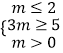 ,即:
,即: ![]()
【解析】(1)分别解出关于p,q的不等式,根据p∧q为真,p,q都为真,求出x的范围即可;(2)由q是p的充分不必要条件,即qp,其逆否命题为pq,求出m的范围即可.
【考点精析】根据题目的已知条件,利用复合命题的真假的相关知识可以得到问题的答案,需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )
A.f(sinA)>f(sinB)
B.f(sinA)>f(cosB)
C.f(cosC)>f(sinB)
D.f(sinC)>f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:
(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率公布直方图中
之间的男生人数,并计算频率公布直方图中![]() 之间的矩形的高;
之间的矩形的高;
(3)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的![]() 的值__________.
的值__________.

【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为![]() 和
和![]() ,高为
,高为![]() ,
,
如图所示, ![]() 平面
平面![]() ,
,
所以底面积为![]() ,
,
几何体的高为![]() ,所以其体积为
,所以其体积为![]() .
.

点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
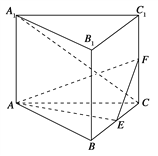
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)=2+sinx,且f(0)=﹣1,数列{an}是以 ![]() 为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则
为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则 ![]() =( )
=( )
A.2016
B.2015
C.2014
D.2013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com