
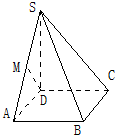
 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.分析 (Ⅰ)证明BC⊥SC,只需证明BC⊥面SDC,根据SD⊥底面ABCD证明SD⊥BC即可;
(Ⅱ)连接BD,∠ADB为二面角A-SD-B的平面角,根据ABCD是正方形,即可得到结论.
(Ⅲ)取AB中点N,连接MN,DN,∠NMD(或其补角)为异面直线DM与SB所成角,计算DM,DN,MN,即可得到结论;
解答 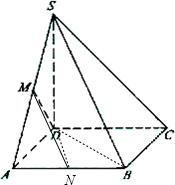 (Ⅰ)证明:∵ABCD是正方形,∴BC⊥CD
(Ⅰ)证明:∵ABCD是正方形,∴BC⊥CD
∵SD⊥底面ABCD,BC?底面ABCD
∴SD⊥BC
∵SD∩CD=D
∴BC⊥面SDC
∵SC?面SDC
∴BC⊥SC;
(Ⅱ)解:连接BD,∵SD⊥底面ABCD,AD,BD?底面ABCD
∴SD⊥AD,SD⊥BD
∴∠ADB为二面角A-SD-B的平面角,
∵ABCD是正方形,
∴∠ADB=45°
∴二面角A-SD-B的平面角为45°,
(Ⅲ)取AB中点N,连接MN,DN,则SB=$\sqrt{3}$
∵正方形ABCD的边长为1,SD⊥底面ABCD,.
∴SD=1
∴DM=$\frac{\sqrt{2}}{2}$,DN=$\frac{\sqrt{5}}{2}$
∵棱SA的中点为M,AB中点N,
∴MN=$\frac{\sqrt{3}}{2}$,MN∥SB
∴∠NMD(或其补角)为异面直线DM与SB所成角
∵DM=$\frac{\sqrt{2}}{2}$,DN=$\frac{\sqrt{5}}{2}$,MN=$\frac{\sqrt{3}}{2}$
∴∠NMD=90°
∴异面直线DM与SB所成角为90°
点评 本题考查线面垂直,线线垂直,考查线线角,面面角,解题的关键是掌握线面垂直的判断,正确找出线线角,面面角,属于中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{36}=1$ | C. | $\frac{x^2}{36}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{49}+\frac{y^2}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,则l平行于α内的所有直线 | B. | 若m?α,l?β且l⊥m,则α⊥β | ||
| C. | 若l?β,l⊥α,则α⊥β | D. | 若m?α,l?β且α∥β,则m∥l |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )| A. | 2$\sqrt{3}$ | B. | 12 | C. | 2$\sqrt{3}$+12 | D. | 2$\sqrt{3}$+6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com