
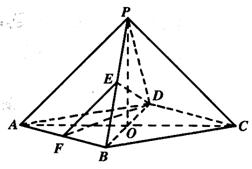
(06年上海卷理)(14分)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
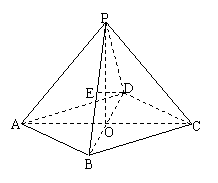
解析:(1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角, ∠PBO=60°.在Rt△AOB中BO=ABsin30°=1, 由PO⊥BO,于是,PO=BOtg60°=![]() ,而底面菱形的面积为2
,而底面菱形的面积为2![]() .
.
∴四棱锥P-ABCD的体积V=![]() ×2
×2![]() ×
×![]() =2.
=2.
(2)解法一:以O为坐标原点,射线OB、OC、OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.
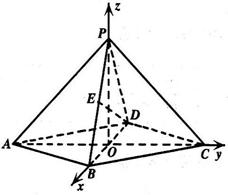 |
在Rt△AOB中OA=![]() ,于是,点A、B、
,于是,点A、B、
D、P的坐标分别是A(0,-![]() ,0),
,0),
B (1,0,0), D (-1,0,0), P (0,0, ![]() ).
).
E是PB的中点,则E(![]() ,0,
,0,![]() ) 于是
) 于是![]() =(
=(![]() ,0,
,0, ![]() ),
),![]() =(0,
=(0, ![]() ,
,![]() ).
).
设![]() 的夹角为θ,有cosθ=
的夹角为θ,有cosθ=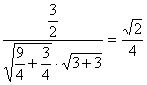 ,θ=arccos
,θ=arccos![]() ,
,
∴异面直线DE与PA所成角的大小是arccos![]() ;
;
解法二:取AB的中点F,连接EF、DF.由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成角(或它的补角),
在Rt△AOB中AO=ABcos30°=![]() =OP,
=OP,
于是, 在等腰Rt△POA中,PA=![]() ,则EF=
,则EF=![]() .
.
在正△ABD和正△PBD中,DE=DF=![]() ,
,
cos∠FED=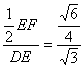 =
=![]()
∴异面直线DE与PA所成角的大小是arccos![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
(06年上海卷理)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
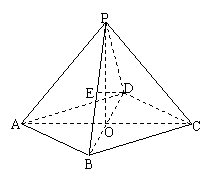
(06年上海卷理)(14分)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年上海卷理)(14分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com