
【题目】已知椭圆 ![]() 的一个焦点与抛物线
的一个焦点与抛物线 ![]() 的焦点F重合,且椭圆短轴的两个端点与F构成正三角形.
的焦点F重合,且椭圆短轴的两个端点与F构成正三角形.
(1)求椭圆的方程;
(2)若过点(1,0)的直线l与椭圆交于不同两点P、Q,试问在x轴上是否存在定点E(m,0),使 ![]() 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
【答案】
(1)解:由题意知抛物线的焦点 ![]() ,∴
,∴ ![]()
又∵椭圆的短轴的两个端点与F构成正三角形,∴b=1,
∴椭圆的方程为 ![]()
(2)解:当直线l的斜率存在时,设其斜率为k,则l的方程为:y=k(x﹣1)
代入椭圆方程,消去y,可得(4k2+1)x2﹣8k2x+4k2﹣4=0
设P(x1,y1),Q(x2,y2),则 ![]()
∵ ![]()
∴ ![]() =m2﹣m(x1+x2)+x1x2+y1y2=
=m2﹣m(x1+x2)+x1x2+y1y2= ![]() =
= ![]() =
= ![]()
= ![]() =
= ![]() …
…
当 ![]() ,即
,即 ![]() 时,
时, ![]() 为定值
为定值 ![]()
当直线l的斜率不存在时, ![]()
由 ![]() 可得
可得 ![]() ,∴
,∴ ![]()
综上所述,当 ![]() 时,
时, ![]() 为定值
为定值 ![]()
【解析】(1)求出抛物线的焦点坐标,可得c,再求出b的值,即可求椭圆的方程;(2)分类讨论,设出直线方程,代入椭圆方程,利用韦达定理,结合向量的数量积公式,即可求得结论.


科目:高中数学 来源: 题型:
【题目】给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种. 
A.21
B.32
C.43
D.54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最大值,则函数y=f(x+
处取得最大值,则函数y=f(x+ ![]() )是( )
)是( )
A.奇函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
C.奇函数且它的图象关于点( ![]() ,0)对称
,0)对称
D.偶函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=xln(﹣x)+(a﹣1)x.
(1)若f(x)在x=﹣e处取得极值,求函数f(x)的单调区间;
(2)求函数f(x)在区间[﹣e2 , ﹣e﹣1]上的最大值g(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x+x2 .
(1)求x<0时,f(x)的解析式;
(2)问是否存在这样的非负数a,b,当x∈[a,b]时,f(x)的值域为[4a﹣2,6b﹣6]?若存在,求出所有的a,b值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
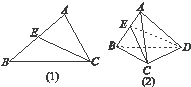
【题目】在平面中,△ABC的角C的内角平分线CE分△ABC面积所成的比 ![]() =
= ![]() .将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,则类比的结论为
.将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,则类比的结论为 ![]() = .
= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com