练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f(x)＝|2x＋4|＋|x－3|.

    (1)解关于x的不等式f(x)<8；

    (2)对于正实数a，b，函数g(x)＝f(x)－3a－4b只有一个零点，求的最小值.

    【答案】（1）(－3，1)；（2）.

    【解析】

    （1）将函数解析式化成分段函数，用分类讨论的方法解不等式.

    （2）作出函数的大致图象，的零点，转化为函数与的交点，由图可知，然后利用基本不等式求的最小值.

    解：（1）由题意可得,

    故当时，不等式可化为，解得，故此时不等式的解集为；

    当时，不等式可化为，解得，故此时不等式的解集为；

    当时，不等式可化为，解得，此时不等式无解,

    综上，不等式的解集为.

    (2)作出函数的大致图象及直线，如图.

    由图可知，当只有一个零点时，，

    即，

    故

    ,

    当且仅当时等号成立．

    的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在矩形中，，，点是边上一点，且，点是的中点，将沿着折起，使点运动到点处，且满足.

    （1）证明：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于曲线，给出下列三个结论：

    ① 曲线关于原点对称，但不关于轴、轴对称；

    ② 曲线恰好经过4个整点（即横、纵坐标均为整数的点）；

    ③ 曲线上任意一点到原点的距离都不大于.

    其中，正确结论的序号是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，得到甲、乙两位学生成绩的茎叶图.

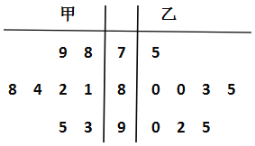
    （1）现要从中选派一人参加数学竞赛，对预赛成绩的平均值和方差进行分析，你认为哪位学生的成绩更稳定？请说明理由；

    （2）若将频率视为概率，求乙同学在一次数学竞赛中成绩高于84分的概率；

    （3）求在甲同学的8次预赛成绩中，从不小于80分的成绩中随机抽取2个成绩，列出所有结果，并求抽出的2个成绩均大于85分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】雷达图(Radar Chart)，又可称为戴布拉图、蜘蛛网图(Spider Chart)，原先是财务分析报表的一种，现可用于对研究对象的多维分析．图为甲、乙两人在五个方面的评价值的雷达图，则下列说法不正确的是（ ）

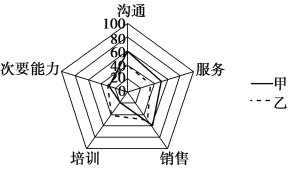
    A.甲、乙两人在次要能力方面的表现基本相同

    B.甲在沟通、服务、销售三个方面的表现优于乙

    C.在培训与销售两个方面上，甲的综合表现优于乙

    D.甲在这五个方面的综合表现优于乙

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年国际篮联篮球世界杯将于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传国际篮联篮球世界杯，某大学从全校学生中随机抽取了120名学生，对是否会收看该国际篮联篮球世界杯赛事的情况进行了问卷调查，统计数据如下：

    会收看

    不会收看

    男生

    60

    20

    女生

    20

    20

    （1）根据上表说明，能否有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关？

    （2）甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球3次均未命中的概率为.

    （i）求乙投球的命中率；

    （ii）若甲投球1次，乙投球2次，两人共命中的次数记为，求的分布列和数学期望.

    附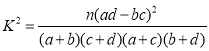：，其中，

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年3月，国内新冠肺炎疫情得到有效控制，人们开始走出家门享受春光.某旅游景点为吸引游客，推出团体购票优惠方案如下表：

    购票人数

    1~50

    51~100

    100以上

    门票价格

    13元/人

    11元/人

    9元/人

    两个旅游团队计划游览该景点.若分别购票，则共需支付门票费1290元；若合并成个团队购票，则需支付门票费990元，那么这两个旅游团队的人数之差为（ ）

    A.20B.30C.35D.40

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当为何值时，轴为曲线的切线；

    （2）用表示、中的最大值，设函数，当时，讨论零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆是椭圆内任一点.设经过的两条不同直线分别于椭圆交于点记的斜率分别为

    （1）当经过椭圆右焦点且为中点时,求:

    ①椭圆的标准方程;

    ②四边形面积的取值范围.

    （2）当时,若点重合于点,且.求证:直线过定点.

    查看答案和解析>>

    同步练习册答案