
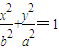 的椭圆E的一个焦点,P、A,B是椭圆E上的点,
的椭圆E的一个焦点,P、A,B是椭圆E上的点,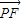 与x轴平行,
与x轴平行,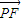 =
=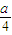 ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),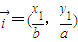 ,
,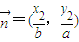 ,
,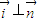 原点O与A、B两点构成的△AOB的面积为S
原点O与A、B两点构成的△AOB的面积为S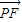 与x轴平行,知
与x轴平行,知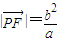 ,由
,由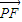 =
= ,知
,知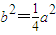 ,由此能求出离心率.
,由此能求出离心率.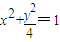 ,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由
,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由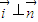 ,知y1=±2x1.S=
,知y1=±2x1.S=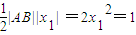 .当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则
.当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则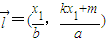 ,
, ,由
,由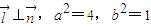 ,知
,知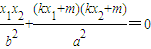 ,由
,由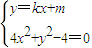 ,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.
,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.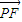 与x轴平行,
与x轴平行,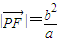 ,
,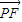 =
=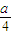 ,
,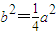 ,
, ,
,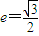 .
.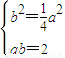 ,得
,得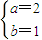 ,
,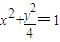 .
.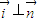 ,
,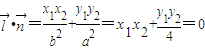 ,
,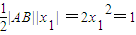 .
.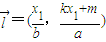 ,
,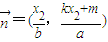 ,
,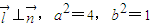 ,
,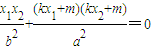 ,
,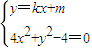 ,得(4+k2)x2+2kmx+m2-4=0,
,得(4+k2)x2+2kmx+m2-4=0,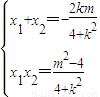 ,
,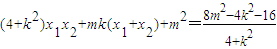 ,
,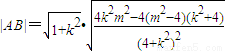
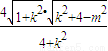
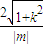 .
.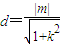 ,
,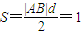 .
.

 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
| x2 |
| b2 |
| y2 |
| a2 |
| PF |
| PF |
| a |
| 4 |
| i |
| x1 |
| b |
| y1 |
| a |
| n |
| x2 |
| b |
| y2 |
| a |
| i |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
| 1+sin2B |
| cos2B-sin2B |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 2 |
| m |
| n |
| 3 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com