
【题目】某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致为( )
A.  B.
B. 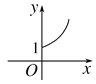 C.
C.  D.
D. 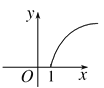
【答案】D
【解析】应选B
分析:根据某林区的森林蓄积量每年比上一年平均增长9.5%,可得经过y年,森林蓄积量,利用要增长到原来的x倍,需经过y年,可建立方程,从而可判断.
解答:解:设原来森林蓄积量为a
∵某林区的森林蓄积量每年比上一年平均增长9.5%,
∴一年后,森林蓄积量为a(1+9.5%)
两年后,森林蓄积量为a(1+9.5%)2,
经过y年,森林蓄积量为a(1+9.5%)y,
∵要增长到原来的x倍,需经过y年,
∴a(1+9.5%)y=ax
∴1.095y=x
将x,y互换,可得反函数为y=1.095x,
∴函数为指数函数,且为增函数,故选B
点评:本题重点考查函数模型的构建,考查反函数,判断函数的类型是关键.


科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
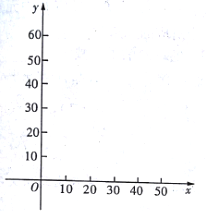
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.

(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=![]() ,AD=CD=1.
,AD=CD=1.
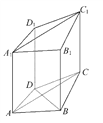
(1)求证:BD⊥AA1.
(2)在棱BC上取一点E,使得AE∥平面DCC1D1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com