
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵f(x)=2x﹣cosx, ∴f(a1)+f(a2)+…+f(a5)=2(a1+a2+…+a5)﹣(cosa1+cosa2+…+cosa5),
∵{an}是公差为 ![]() 的等差数列,
的等差数列,
∴a1+a2+…+a5=5a3 , 由和差化积公式可得,
cosa1+cosa2+…+cosa5
=(cosa1+cosa5)+(cosa2+cosa4)+cosa3
=[cos(a3﹣ ![]() ×2)+cos(a3+
×2)+cos(a3+ ![]() ×2)]+[cos(a3﹣
×2)]+[cos(a3﹣ ![]() )+cos(a3+
)+cos(a3+ ![]() )]+cosa3
)]+cosa3
=2cosa3cos ![]() +2cosa3cos(﹣
+2cosa3cos(﹣ ![]() )+cosa3=cosa3(1+
)+cosa3=cosa3(1+ ![]() +
+ ![]() ),
),
则cosa1+cosa2+…+cosa5的结果不含π,
又∵f(a1)+f(a2)+…+f(a5)=5π,
∴cosa3=0,故a3= ![]() .
.
[f(a3)]2﹣a1a5=π2﹣( ![]() ﹣2
﹣2 ![]() )
) ![]() =
= ![]() .
.
故选:D.
【考点精析】本题主要考查了等差数列的性质的相关知识点,需要掌握在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,且
,且![]() ,公比大于1的等比数列
,公比大于1的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(1)求证数列![]() 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)在(2)的条件下,若![]() 对一切正整数n恒成立,求实数t的取值范围.
对一切正整数n恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() 到抛物线
到抛物线![]() 的焦点
的焦点![]() 的距离等于2.
的距离等于2.
求抛物线![]() 的方程;
的方程;
若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() 为坐标原点),求证直线
为坐标原点),求证直线![]() 恒过
恒过![]() 轴上的某定点,并求出该定点坐标.
轴上的某定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲![]() 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为![]() 万元,且
万元,且![]() (
(![]() ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为![]() (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;
(2)为了让年利润![]() 不低于2360万元,求年产量
不低于2360万元,求年产量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
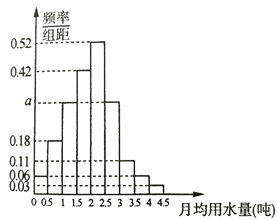
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到0.01),并说明理由.
的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1(3+m)x+4y=5﹣3m,l2 2x+(5+m)y=8.当m分别为何值时,l1与l2:
(1)相交?
(2)平行?
(3)垂直?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com