
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ①③是双底数列,②不是双底数列(2) ![]()
![]() (3)存在整数
(3)存在整数![]() 或
或![]() ,使得数列
,使得数列![]() 为双底数列
为双底数列
【解析】试题分析:(1)根据双底数列的定义可判定①③是双底数列,②不是双底数列;(2)由双底数列定义可知![]() ,解得
,解得![]() , 当
, 当![]() 时,数列成等差,
时,数列成等差, ![]() ,当
,当![]() 时,
时, ![]() ,从而可得结果;(3)
,从而可得结果;(3)![]() , 若数列
, 若数列![]() 是双底数列,则
是双底数列,则![]() 有解(否则不是双底数列),即
有解(否则不是双底数列),即 ![]() ,该方程共有四组解,分别验证是否为双底数列即可得结果.
,该方程共有四组解,分别验证是否为双底数列即可得结果.
试题解析:(1)①③是双底数列,②不是双底数列;
(2)数列![]() 当
当![]() 时递减,当
时递减,当![]() 时递增,
时递增,
由双底数列定义可知![]() ,解得
,解得![]() ,
,
当![]() 时,数列成等差,
时,数列成等差, ![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
综上, ![]() .
.
(3)![]() ,
,
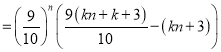
![]() ,
,
若数列![]() 是双底数列,则
是双底数列,则![]() 有解(否则不是双底数列),
有解(否则不是双底数列),
即 ![]() ,
,
得![]() 或
或![]() 或
或![]() 或
或![]()
故当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
从而 ![]() ,数列
,数列![]() 不是双底数列;
不是双底数列;
同理可得:
当![]() 时,
时, ![]() ,数列
,数列![]() 不是双底数列;
不是双底数列;
当![]() 时,
时, ![]() ,数列
,数列![]() 是双底数列;
是双底数列;
当![]() 时,
时, ![]() ,数列
,数列![]() 是双底数列;
是双底数列;
综上,存在整数![]() 或
或![]() ,使得数列
,使得数列![]() 为双底数列.
为双底数列.


科目:高中数学 来源: 题型:
【题目】中国诗词大会的播出引发了全民读书热,某学校语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如右图,若规定得分不低于85分的学生得到“诗词达人”的称号,低于85分且不低于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号.根据该次比赛的成绩按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地相距![]() 海里,某货轮匀速行驶从甲地运输货物到乙地,运输成本包括燃料费用和其他费用.已知该货轮每小时的燃料费与其速度的平方成正比,比例系数为
海里,某货轮匀速行驶从甲地运输货物到乙地,运输成本包括燃料费用和其他费用.已知该货轮每小时的燃料费与其速度的平方成正比,比例系数为![]() ,其他费用为每小时
,其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(![]() )请将该货轮从甲地到乙地的运输成本
)请将该货轮从甲地到乙地的运输成本![]() 表示为航行速度
表示为航行速度![]() (海里/小时)的函数.
(海里/小时)的函数.
(![]() )要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin 2x+![]() cos 2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移
cos 2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移![]() 个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴方程是( )
个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴方程是( )
A. x=-![]() B. x=
B. x=![]()
C. x=![]() D. x=
D. x=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上的一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为![]() ,设这条最短路线与CC1的交点为N.求:
,设这条最短路线与CC1的交点为N.求:

(1)该三棱柱的侧面展开图的对角线的长;
(2)PC和NC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
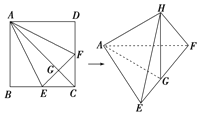
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
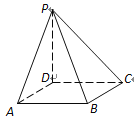
【题目】在四棱锥P–ABCD中,底面ABCD是边长为6的正方形,PD平面ABCD,PD=8.
(1) 求PB与平面ABCD所成角的大小;
(2) 求异面直线PB与DC所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com