
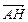 =
=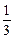
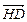 .
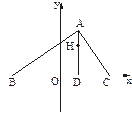
.
 ,
,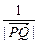 ,
, 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由. +
+ =1(y≠0).
=1(y≠0). (2)见解析
(2)见解析 y).
y). =(x+2,y),
=(x+2,y),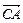 =(x-2,
=(x-2, y).
y). y2=0,即
y2=0,即 +
+  =1,
=1, +
+ =1(y≠0).
=1(y≠0).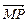 |+|
|+| |=4,|
|=4,| |=2.
|=2. ,
,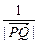 ,
, 成等差数列,则
成等差数列,则 +
+ =
= =1.
=1.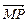 |·|
|·| |="|"
|="|" 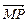 |+|
|+| |=4.
|=4. 可得|
可得|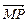 |=|
|=| |=2,
|=2, +
+ =1的短轴端点.
=1的短轴端点.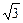 )或(0,-
)或(0,-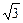 )时,
)时, ,
,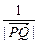 ,
, 成等差数列.
成等差数列. +
+  =1的两个焦点,
=1的两个焦点,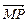 |+|
|+| |="4,|"
|="4,|"  |=2.
|=2. ,
,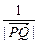 ,
, 成等差数列,
成等差数列, +
+ =
= =1.
=1.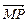 |=a+ex,|
|=a+ex,| |=a-ex,
|=a-ex, +
+ =1.解得x=0.
=1.解得x=0.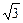 )或(0,-
)或(0,-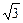 ).
).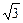 )或(0,-
)或(0,-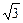 )时,
)时, ,
,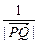 ,
, 成等差数列.
成等差数列.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 d,
d, ≤d≤
≤d≤ .
. ·
· =
= ,求向量
,求向量 与
与 的夹角.
的夹角.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com