
【题目】如图,在底面为平行四边形的四棱锥![]() 中,过点
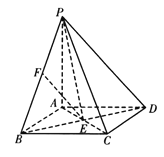
中,过点![]() 的三条棱PA、AB、AD两两垂直且相等,E,F分别是AC,PB的中点.
的三条棱PA、AB、AD两两垂直且相等,E,F分别是AC,PB的中点.

(Ⅰ)证明:EF//平面PCD;
(Ⅱ)求EF与平面PAC所成角的大小.
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】
(Ⅰ)连接BD,则E是BD的中点,F是PB的中点得EF//PD。线面平行转化为线线平行。
(Ⅱ)首先找出EF与平面PAC所成的角,由题意可得EF与平面PAC所成的角的大小等于![]() 。根据条件得
。根据条件得![]() ,所以
,所以![]() 。
。
(Ⅰ)证明:如图,连接BD,则E是BD的中点
又F是PB的中点,∴ EF//PD,
∵ EF不在平面PCD内,∴ EF//平面PCD。
(Ⅱ)连接PE,∵ ABCD是正方形,∴![]()
又![]() 平面
平面![]() ,∴
,∴![]() 。
。
∴![]() 平面
平面![]() ,故
,故![]() 是PD与平面PAC所成的角,
是PD与平面PAC所成的角,
∵EF//PD,∴EF与平面PAC所成的角的大小等于![]()
∵PA=AB=AD,![]() ,
,
∴![]() ≌
≌![]() ,因此PD=BD
,因此PD=BD
在![]() 中,
中,![]() ,
,![]()
∴EF与平面PAC所成角的大小是![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0)满足f(0)=0,对于任意x∈R,都有f(x)≥x,且![]() ,令g(x)=f(x)﹣|λx﹣1|(λ>0).
,令g(x)=f(x)﹣|λx﹣1|(λ>0).
(1)求函数f(x)的表达式;
(2)求函数g(x)的单调区间;
(3)当λ>2时,判断函数g(x)在区间(0,1)上的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ) (参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
A.12
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆[x﹣(e+ ![]() )]2+y2=1任意一点,则线段PQ的长度的最小值为( )
)]2+y2=1任意一点,则线段PQ的长度的最小值为( )
A.![]()
B.![]()
C.![]()
D.e+ ![]() ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2. 
(1)求证:BD⊥平面ADE;
(2)求直线BE和平面CDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式:|2x﹣m|≤1的整数解有且仅有一个值为2.
(Ⅰ)求整数m的值;
(Ⅱ)已知a,b,c∈R,若4a4+4b4+4c4=m,求a2+b2+c2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com