
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
【答案】![]()
【解析】
根据题意可知函数f(x)是一个周期为2e的偶函数,即可作出函数f(x)在[﹣e,3e]上的图象,由方程的根与两函数图象交点的横坐标的关系可求得![]() 的值,再利用二倍角公式化简函数
的值,再利用二倍角公式化简函数![]() ,然后根据平移法则即可求得
,然后根据平移法则即可求得![]() ,从而求得
,从而求得![]() .
.
因为f(e+x)=f(e﹣x),所以f(x)关于x=e对称,又因为偶函数f(x),
所以f(x)的周期为2e.
当x∈(0,e]时,f(x)=lnx,于是可作出函数f(x)在[﹣e,3e]上的图象如图所示,
方程![]() 的实数根是函数y=f(x)与函数
的实数根是函数y=f(x)与函数![]() 的交点的横坐标,
的交点的横坐标,
由图象的对称性可知,两个函数在[﹣e,3e]上有4个交点,且4个交点的横坐标之和为4e,所以4e=3ea,故a![]() ,
,
因为![]() ,
,
所以![]() ,
,
故![]() .
.
故答案为:![]() .
.



 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,在以坐标原点为极点,
,在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从洛阳的高中生中,随机抽取了55人,从上海的高中生中随机抽取了45人进行答题.洛阳高中生答题情况是:选择家的占![]() 、选择朋友聚集的地方的占
、选择朋友聚集的地方的占![]() 、选择个人空间的占
、选择个人空间的占![]() .上海高中生答题情况是:选择朋友聚集的地方的占
.上海高中生答题情况是:选择朋友聚集的地方的占![]() 、选择家的占
、选择家的占![]() 、选择个人空间的占
、选择个人空间的占![]() .
.
(1)请根据以上调查结果将下面![]() 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有![]() 的把握认为“恋家(在家里感到最幸福)”与城市有关:
的把握认为“恋家(在家里感到最幸福)”与城市有关:
在家里最幸福 | 在其它场所最幸福 | 合计 | |
洛阳高中生 | |||
上海高中生 | |||
合计 |
(2) 从被调查的不“恋家”的上海学生中,用分层抽样的方法选出4人接受进一步调查,从被选出的4 人中随机抽取2人到洛阳交流学习,求这2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() d.
d.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
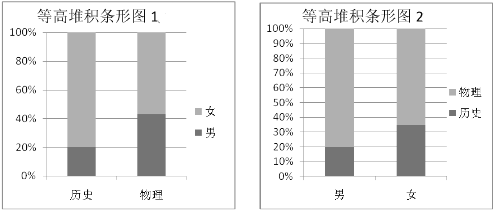
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作.其中的一道题“今有木,方三尺,高三尺,欲方五寸作枕一枚.问:得几何?”意思是:“有一块棱长为3尺的正方体方木,要把它作成边长为5寸的正方体枕头,可作多少个?”现有这样的一个正方体木料,其外周已涂上油漆,则从切割后的正方体枕头中任取一块,恰有一面涂上油漆的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义“
,定义“![]() 变换”:
变换”:![]() 将数列
将数列![]() 变换成数列
变换成数列![]() ,其中
,其中![]() ,且
,且![]() ,这种“
,这种“![]() 变换”记作
变换”记作![]() .继续对数列
.继续对数列![]() 进行“
进行“![]() 变换”,得到数列
变换”,得到数列![]() ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为![]() 时变换结束.
时变换结束.
(1)试问![]() 和
和![]() 经过不断的“
经过不断的“![]() 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“![]() 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(2)求![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;
(3)证明:![]() 一定能经过有限次“
一定能经过有限次“![]() 变换”后结束.
变换”后结束.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com