解:(I)f(x)的定义域为(0,+∞),
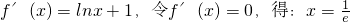
,
当x∈(0,+∞)时,f'(x),f(x)的变化的情况如下:
∴由表格可知:函数f(x)在区间(0,+∞)上有唯一的极小值,因此也是最小值.
即

.
(II) 由题意得:f'(x)=lnx+a+1,
∵函数f(x)在区间[e
2,+∞)上为增函数,∴当x∈[e
2,+∞)时f'(x)≥0,即lnx+a+1≥0在[e
2,+∞)上恒成立,∴a≥-1-lnx,
又当x∈[e
2,+∞)时,lnx∈[2,+∞),∴-1-lnx∈(-∞,-3],
∴a≥-3.
(III)原不等式可化为:f(a)+f[(a+b)-a]≥f(a+b)-(a+b)ln2,
设函数g(x)=f(x)+f(k-x)(k>0).
则g(x)=xlnx+(k-x)ln(k-x)(0<x<k),
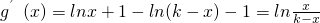
,
令g
′(x)>0,则
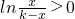
,∴

,∴

,解得
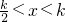
.
令

,
∴
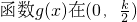
上单调递减,在
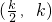
上单调递增,
∴g(x)在(0,k)上的最小值为

,
∴当x∈(0,k)时,总有
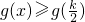
,
即f(x)+f(k-x)≥
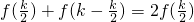
=
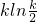
=klnk-kln2=f(k)-kln2
令x=a,k-x=b,则有:f(a)+f(b)≥f(a+b)-(a+b)ln2.
分析:(I)利用导数与函数单调性的关系定理即可得出极小值,进而得到最小值.
(II)函数f(x)在区间[e
2,+∞)上为增函数?当x∈[e
2,+∞)时f'(x)≥0?lnx+a+1≥0在[e
2,+∞)上恒成立?a≥[-1-lnx]
max,x∈[e
2,+∞).解出即可.
(III)原不等式可化为:f(a)+f[(a+b)-a]≥f(a+b)-(a+b)ln2,设函数g(x)=f(x)+f(k-x)(k>0).利用导数研究其单调性即可证明结论.
点评:本题综合考查了利用导数研究函数的单调性、极值、最值等性质,及其等价转化、构造函数法等基本技能.需要较好的观察力和计算能力.

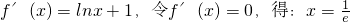 ,
,


 .
.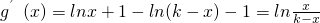 ,
,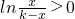 ,∴
,∴ ,∴
,∴ ,解得
,解得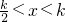 .
. ,
,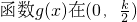 上单调递减,在
上单调递减,在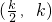 上单调递增,
上单调递增, ,
,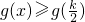 ,
,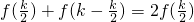 =
=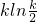 =klnk-kln2=f(k)-kln2
=klnk-kln2=f(k)-kln2

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<