
【题目】如图,在正方体ABCD﹣A1B1C1D1中,
(1)求证:AD1⊥平面CDA1B1;
(2)求直线AD1与直线BD所成的角.
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=4
(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x﹣y+1=0与圆C交于A、B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)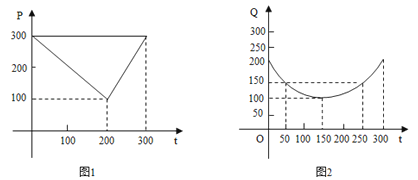
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过圆上任意一点
过圆上任意一点![]() 向
向![]() 轴引垂线垂足为
轴引垂线垂足为![]() (点
(点![]() 、
、![]() 可重合),点
可重合),点![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹方程为曲线
的轨迹方程为曲线![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,满足直线
两点,满足直线![]() ,
, ![]() ,
, ![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,(
,( ![]() ),设
),设![]()
(1)若![]() ,求证:
,求证: ![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若![]() ,又数列
,又数列![]() 满足:
满足: ![]() :
:
①求数列![]() 的前
的前![]() 和
和![]() ;
;
②求证:数列![]() 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com