
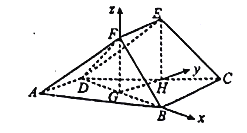
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是平行四边形,平面
是平行四边形,平面![]() 平面
平面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() .
.
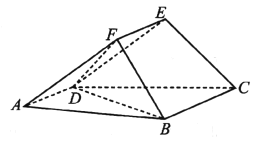
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)分别取![]() ,
,![]() 的中点连结
的中点连结![]() ,
,![]() ,
,![]() ,先证
,先证![]() ,再证
,再证![]() 平面
平面![]() ,然后可得
,然后可得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,可证平面
,可证平面![]() 平面
平面![]() ;
;
(2)先建立空间直角坐标系,然后分别求出平面![]() 的法向量为
的法向量为![]() 和平面
和平面![]() 的法向量为
的法向量为![]() ,然后代入公式
,然后代入公式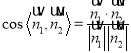 计算即可.
计算即可.
(1)如图,分别取![]() ,
,![]() 的中点连结
的中点连结![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
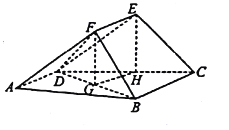
∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
又![]() 为正三角形,
为正三角形,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
满足![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)由(1)得建立如图所示的空间直角坐标系![]() ,
,
由题意得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
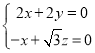 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
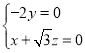 ,解得
,解得![]() ,令
,令![]() ,则
,则![]() ,
,
∴![]() ,
,
∴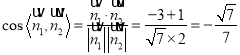 ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】正态分布有极其广泛的实际背景,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如,同一种生物体的身长、体重等指标.随着“绿水青山就是金山银山”的观念不断的深入人心,环保工作快速推进,很多地方的环境出现了可喜的变化.为了调查某水库的环境保护情况,在水库中随机捕捞了100条鱼称重.经整理分析后发现,鱼的重量x(单位:kg)近似服从正态分布![]() ,如图所示,已知
,如图所示,已知![]() .
.
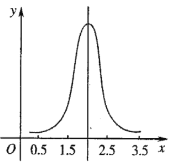
(Ⅰ)若从水库中随机捕捞一条鱼,求鱼的重量在![]() 内的概率;
内的概率;
(Ⅱ)(ⅰ)从捕捞的100条鱼中随机挑出6条鱼测量体重,6条鱼的重量情况如表.
重量范围(单位:kg) |
|
|
|
条数 | 1 | 3 | 2 |
为了进一步了解鱼的生理指标情况,从6条鱼中随机选出3条,记随机选出的3条鱼中体重在![]() 内的条数为X,求随机变量X的分布列和数学期望;
内的条数为X,求随机变量X的分布列和数学期望;
(ⅱ)若将选剩下的94条鱼称重做标记后立即放生.两周后又随机捕捞1000条鱼,发现其中带有标记的有2条.为了调整生态结构,促进种群的优化,预备捕捞体重在![]() 内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在
内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在![]() 内的鱼的条数.
内的鱼的条数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为平面直角坐标系
为平面直角坐标系![]() 中的一个动点(其中
中的一个动点(其中![]() 为坐标系原点),点
为坐标系原点),点![]() 到定点
到定点![]() 的距离比到直线
的距离比到直线![]() 的距离大1,动点
的距离大1,动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
①若![]() ,求直线
,求直线![]() 的直线方程;
的直线方程;
②分别过点![]() ,
,![]() 作曲线
作曲线![]() 的切线且交于点
的切线且交于点![]() ,是否存在以
,是否存在以![]() 为圆心,以
为圆心,以![]() 为半径的圆与经过点
为半径的圆与经过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
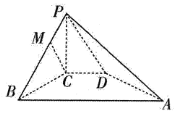
(1)求证:![]() 面
面![]() :
:
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com