
【题目】设函数![]() ,
,![]() ,(其中
,(其中![]() ).
).
(1)![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)证:存在![]() ,使得
,使得![]() 在
在![]() 内恒成立,且方程
内恒成立,且方程![]() 在
在![]() 内有唯一解.
内有唯一解.
【答案】(1) ![]() ;
;![]() ;(2)见解析.
;(2)见解析.
【解析】
(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)求出f(x)的导数,通过讨论m的范围,求出f(x)的单调区间,求出满足条件的m的范围,从而证出结论即可.
解:(I)当![]() 时,
时, ![]() ,
,![]()
令![]() ,得
,得![]() ,
,![]() ,当
,当![]() 变化时,
变化时,![]() 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
由表可知,![]() ;
;![]() ;
;
(II)设![]() ,
,![]() ,
,![]() ,若
,若![]() 要有解,需
要有解,需![]() 有单减区间,则
有单减区间,则![]() 要有解
要有解
![]() ,由
,由![]() ,
,![]() ,记
,记![]() 为函数
为函数![]() 的导数
的导数
则![]()
![]() ,当
,当![]() 时
时![]() 单增,令
单增,令![]() ,由
,由![]() ,得
,得![]() ,需考察
,需考察![]() 与区间
与区间![]() 的关系:
的关系:
①当![]() 时,
时,![]() ,
,![]() ,在
,在![]() 上
上![]() ,
,![]() 单增,
单增,![]()
故![]() 单增,
单增,![]() ,
,![]() 无解;
无解;
②当![]() ,时,
,时,![]() ,
,![]() ,因为
,因为![]() 单增,在
单增,在![]() 上
上![]() ,在
,在![]() 上
上![]()
当![]() 时,
时,![]()
![]()
(i)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() 单增,
单增,![]() ,
,![]() 无解;
无解;
(ii)若![]() ,即
,即![]() ,
,![]() ,在
,在![]() 上,
上,![]() ,
,![]() 单减;
单减;![]() ,
,![]() ,
,![]() 在区间
在区间![]() 上有唯一解,记为
上有唯一解,记为![]() ;在
;在![]() 上,
上,![]() 单增 ,
单增 ,![]() ,当
,当![]() 时
时![]() ,故
,故![]() 在区间
在区间![]() 上有唯一解,记为
上有唯一解,记为![]() ,则在
,则在![]() 上
上![]() ,在
,在![]() 上
上![]() ,在
,在![]() 上
上![]() ,当
,当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时
,此时![]()
若要![]() 恒成立且
恒成立且![]() 有唯一解,当且仅当
有唯一解,当且仅当![]() ,即
,即![]() ,由
,由![]() 有
有![]()
联立两式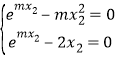 解得
解得![]() .综上,当
.综上,当![]() 时,
时,![]()


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 
(1)求x的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关? 附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 为下述条件的函数
为下述条件的函数![]() 的集合:①定义域为
的集合:①定义域为![]() ;②对任意实数
;②对任意实数![]() ,都有
,都有![]() .
.
(1)判断函数![]() 是否为
是否为![]() 中元素,并说明理由;
中元素,并说明理由;
(2)若函数![]() 是奇函数,证明:
是奇函数,证明:![]() ;
;
(3)设![]() 和
和![]() 都是
都是![]() 中的元素,求证:
中的元素,求证: 也是
也是![]() 中的元素,并举例说明,
中的元素,并举例说明, 不一定是
不一定是![]() 中的元素.
中的元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90℃,BC=2AD,△PAB与△PAD都是等边三角形,平面ABCD⊥平面PBD.
(I)证明:CD⊥平面PBD;
(II)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数y=f(x)的导函数的图象如图所示,给出下列判断:

①函数y=f(x)在区间(-3,-1)内单调递增;②当x=2时,函数y=f(x)有极小值;
③函数y=f(x)在区间![]() 内单调递增;④当
内单调递增;④当![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是( )
A. ①② B. ②③ C. ③④ D. ③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() sin
sin ![]() ,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
A.(﹣∞,﹣6)∪(6,+∞)
B.(﹣∞,﹣4)∪(4,+∞)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com